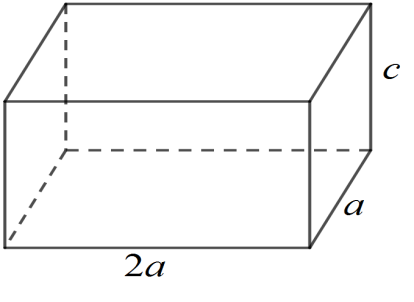
Ông An muốn xây một cái bể chứa nước lớn dạng một khối hộp chữ nhật không nắp có thể tích bằng $288{{\text{m}}^{3}}$. Đáy bể là hình chữ nhật có chiều dài gấp đôi chiều rộng, giá thuê nhân công để xây bể là $500000$ đồng/ ${{\text{m}}^{\text{2}}}$. Ba kích thước của bể được mô tả như hình vẽ dưới $\left( a\left( m \right){>}0,c\left( m \right){>}0 \right)$.
Nếu ông An biết xác định các kích thước của bể hợp lí thì chi phí thuê nhân công sẽ thấp nhất và (Biết độ dày thành bể và đáy bể không đáng kể). Khi đó:
a) Diện tích các mặt cần xây là $S=2{{a}^{2}}+5ac$.
b) $2{{a}^{2}}c=288$.
c) Diện tích các mặt cần xây nhỏ nhất là $216{{\text{m}}^{2}}$.
d) Chi phí thấp nhất để xây dựng bể đó là $100$ triệu đồng.
Lời giải: Từ hình vẽ ta có ba kích thước của bể là $a$, $2a$, $c$.
Ta có diện tích cách mặt cần xây là $S=2{{a}^{2}}+4ac+2ac=2{{a}^{2}}+6ac$.Thể tích bể $V=a \cdot 2a \cdot c=2{{a}^{2}}c=288\left( 1 \right)$ Từ $\left( 1 \right)$ $\Rightarrow c=\dfrac{144}{{{a}^{2}}}$ nên $S=2{{a}^{2}}+6a \cdot \dfrac{144}{{{a}^{2}}}=2{{a}^{2}}+\dfrac{864}{a}$.
Xét hàm số $S\left( a \right)=2{{a}^{2}}+\dfrac{864}{a}\Rightarrow {S}’\left( a \right)=4a-\dfrac{864}{{{a}^{2}}}$.
${S}’\left( a \right)=0\Leftrightarrow 4a-\dfrac{864}{{{a}^{2}}}=0\Leftrightarrow {{a}^{3}}=216\Leftrightarrow a=6$
Bảng biến thiên của hàm số $S\left( a \right)=2{{a}^{2}}+\dfrac{864}{a}\left( a{>}0 \right)$
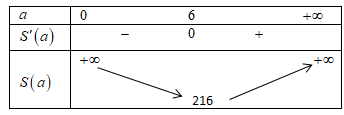
${{S}_{\min }}=216{{\text{m}}^{2}}$, khi đó chi phí thấp nhất là $216 \cdot 500000=108$ triệu đồng.
(Sai) Diện tích các mặt cần xây là $S=2{{a}^{2}}+5ac$.
(Vì): Diện tích các mặt cần xây là $S=2{{a}^{2}}+4ac+2ac=2{{a}^{2}}+6ac$.
(Đúng) $2{{a}^{2}}c=288$.
(Đúng) Diện tích các mặt cần xây nhỏ nhất là $216{{\text{m}}^{2}}$.
(Vì): Theo lời giải, ${{S}_{\min }}=216{{\text{m}}^{2}}$.
(Sai) Chi phí thấp nhất để xây dựng bể đó là $100$ triệu đồng.
(Vì): Theo lời giải, chi phí thấp nhất là $216 \cdot 500000 = 108$ triệu đồng.
