Cho một tấm nhôm hình vuông cạnh a. Người ta cắt ở 4 góc 4 hình vuông bằng nhau, rồi gập tấm nhôm lại để được một cái hộp không nắp.

Cho một tấm nhôm hình vuông cạnh a. Người ta cắt ở 4 góc 4 hình vuông bằng nhau, rồi gập tấm nhôm lại để được một cái hộp không nắp.

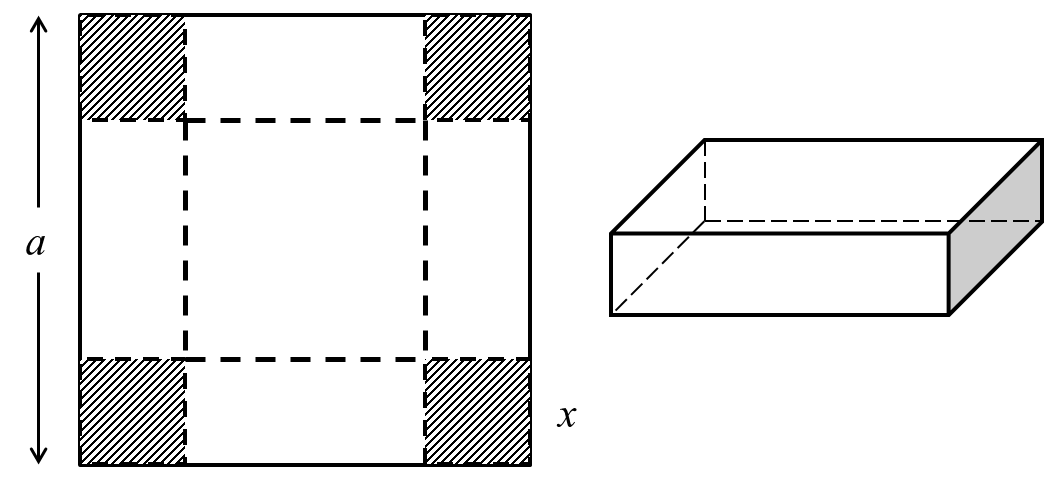
a) Thể tích của khối hộp là lớn nhất khi cạnh của hình vuông bị cắt bằng $\dfrac{a}{12}$.

b) Thể tích của khối hộp là lớn nhất khi cạnh của hình vuông bị cắt bằng $\dfrac{a}{12}$.

c) Thể tích của khối hộp lớn nhất bằng $\dfrac{{{a}^{3}}}{27}.$.

d) Thể tích hộp lớn nhất bằng $\dfrac{2{{a}^{3}}}{27}.$.

Lời giải:

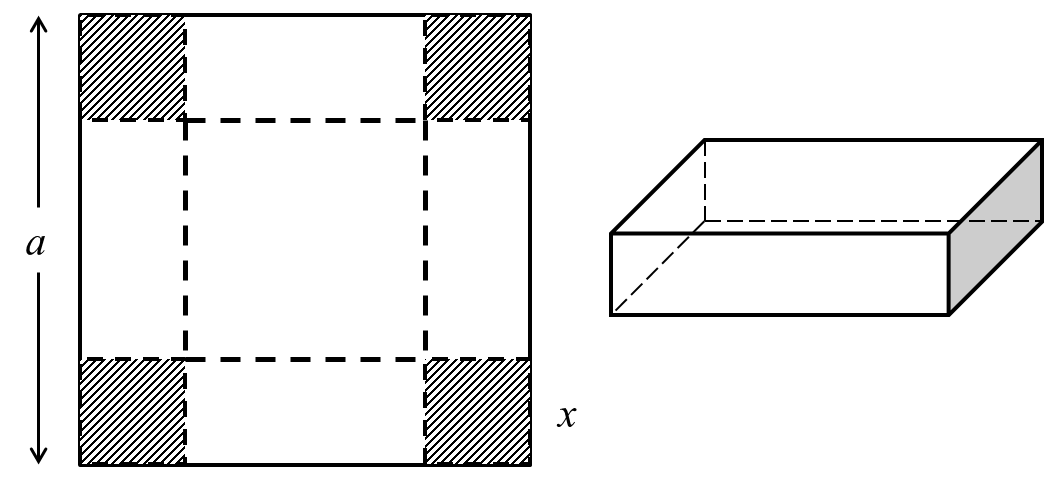
Gọi $x$ là độ dài cạnh của hình vuông bị cắt $\left( 0{<}x{
Thể tích của khối hộp là: $V\left( x \right)=x{{\left( a-2x \right)}^{2}}$ $\left( 0{<}x{
${V}’\left( x \right)={{\left( a-2x \right)}^{2}}+x.2\left( a-2x \right).\left( -2 \right)=\left( a-2x \right)\left( a-6x \right)$ $=0\Leftrightarrow x=\dfrac{a}{6}$ $\left( 0{<}x{
Bảng biến thiên:

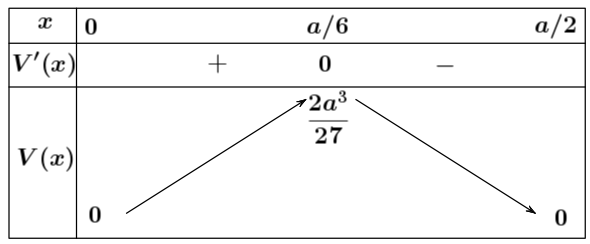
Vậy $\lim\limits_{\left( 0;\dfrac{a}{2} \right)}V(x)=V\left( \dfrac{a}{6} \right)=\dfrac{2{{a}^{3}}}{27}$.
(a) Sai: Thể tích của khối hộp là lớn nhất khi cạnh của hình vuông bị cắt bằng $\dfrac{a}{12}$.
(b) Đúng: Thể tích của khối hộp là lớn nhất khi cạnh của hình vuông bị cắt bằng $\dfrac{a}{6}$.
(c) Đúng: Thể tích của khối hộp lớn nhất bằng $\dfrac{2{{a}^{3}}}{27}.$
(d) Sai: Thể tích hộp lớn nhất bằng $\dfrac{{{a}^{3}}}{27}.$
(Sai) Thể tích của khối hộp là lớn nhất khi cạnh của hình vuông bị cắt bằng $\dfrac{a}{12}$.
(Vì): Gọi $x$ là độ dài cạnh của hình vuông bị cắt $\left( 0{<}x{
Thể tích của khối hộp là: $V\left( x \right)=x{{\left( a-2x \right)}^{2}}$ $\left( 0{<}x{
${V}’\left( x \right)={{\left( a-2x \right)}^{2}}+x.2\left( a-2x \right).\left( -2 \right)=\left( a-2x \right)\left( a-6x \right)$ $=0\Leftrightarrow x=\dfrac{a}{6}$ $\left( 0{<}x{
Bảng biến thiên:

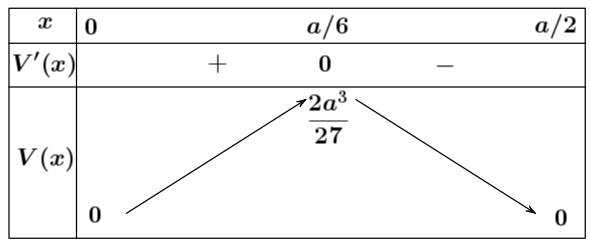
Vậy $\lim\limits_{\left( 0;\dfrac{a}{2} \right)}V(x)=V\left( \dfrac{a}{6} \right)=\dfrac{2{{a}^{3}}}{27}$.
(Sai) Thể tích của khối hộp là lớn nhất khi cạnh của hình vuông bị cắt bằng $\dfrac{a}{12}$.
(Vì): Gọi $x$ là độ dài cạnh của hình vuông bị cắt $\left( 0{<}x{
Thể tích của khối hộp là: $V\left( x \right)=x{{\left( a-2x \right)}^{2}}$ $\left( 0{<}x{
${V}’\left( x \right)={{\left( a-2x \right)}^{2}}+x.2\left( a-2x \right).\left( -2 \right)=\left( a-2x \right)\left( a-6x \right)$ $=0\Leftrightarrow x=\dfrac{a}{6}$ $\left( 0{<}x{
Bảng biến thiên:

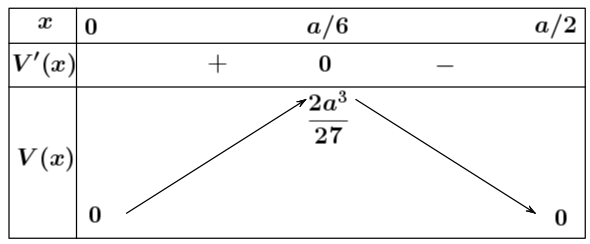
Vậy $\lim\limits_{\left( 0;\dfrac{a}{2} \right)}V(x)=V\left( \dfrac{a}{6} \right)=\dfrac{2{{a}^{3}}}{27}$.
(Sai) Thể tích của khối hộp lớn nhất bằng $\dfrac{{{a}^{3}}}{27}.$
(Vì): Gọi $x$ là độ dài cạnh của hình vuông bị cắt $\left( 0{<}x{
Thể tích của khối hộp là: $V\left( x \right)=x{{\left( a-2x \right)}^{2}}$ $\left( 0{<}x{
${V}’\left( x \right)={{\left( a-2x \right)}^{2}}+x.2\left( a-2x \right).\left( -2 \right)=\left( a-2x \right)\left( a-6x \right)$ $=0\Leftrightarrow x=\dfrac{a}{6}$ $\left( 0{<}x{
Bảng biến thiên:

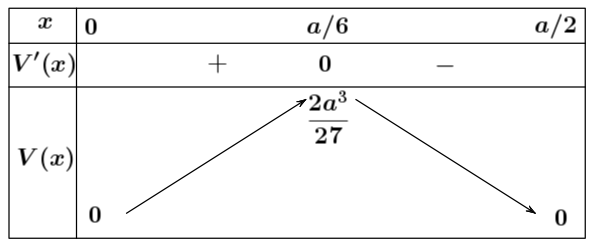
Vậy $\lim\limits_{\left( 0;\dfrac{a}{2} \right)}V(x)=V\left( \dfrac{a}{6} \right)=\dfrac{2{{a}^{3}}}{27}$.
(Đúng) Thể tích hộp lớn nhất bằng $\dfrac{2{{a}^{3}}}{27}.$
(Vì): Gọi $x$ là độ dài cạnh của hình vuông bị cắt $\left( 0{<}x{
Thể tích của khối hộp là: $V\left( x \right)=x{{\left( a-2x \right)}^{2}}$ $\left( 0{<}x{
${V}’\left( x \right)={{\left( a-2x \right)}^{2}}+x.2\left( a-2x \right).\left( -2 \right)=\left( a-2x \right)\left( a-6x \right)$ $=0\Leftrightarrow x=\dfrac{a}{6}$ $\left( 0{<}x{
Bảng biến thiên:

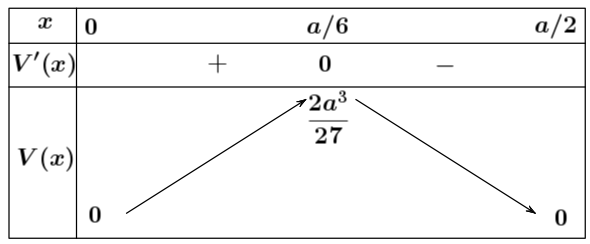
Vậy $\lim\limits_{\left( 0;\dfrac{a}{2} \right)}V(x)=V\left( \dfrac{a}{6} \right)=\dfrac{2{{a}^{3}}}{27}$.