Cho hàm số $f\left( x \right)=2{{x}^{2}}+\dfrac{500}{x}$. Hàm số đạt

a) Giá trị nhỏ nhất là 150 trên $\left( 0;+\infty \right)$

Cho hàm số $f\left( x \right)=2{{x}^{2}}+\dfrac{500}{x}$. Hàm số đạt

a) Giá trị nhỏ nhất là 150 trên $\left( 0;+\infty \right)$.
.

b) Giá trị nhỏ nhất là 150 trên $\left( 0;+\infty \right)$.
.

c) Giá trị lớn nhất là 502 trên $\left( 0;5 \right]$.
.

d) Hàm số không có giá trị lớn nhất trên $\left( 0;+\infty \right)$.
.

Lời giải: ${f}’\left( x \right)=4x-\dfrac{500}{{{x}^{2}}}=\dfrac{4{{x}^{3}}-500}{{{x}^{2}}}$, ${f}’\left( x \right)=0\Leftrightarrow 4{{x}^{3}}-500=0\Leftrightarrow x=5$.
Bảng biến thiên.

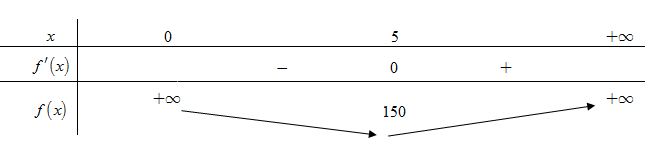
(Đúng) Giá trị nhỏ nhất là 150 trên $\left( 0;+\infty \right)$.

(Vì): Từ bảng biến thiên, ta thấy hàm số đạt giá trị nhỏ nhất là $150$ tại $x=5$ trên khoảng $\left( 0;+\infty \right)$.
(Đúng) Giá trị nhỏ nhất là 150 trên $\left( 0;+\infty \right)$.

(Vì): Từ bảng biến thiên, ta thấy hàm số đạt giá trị nhỏ nhất là $150$ tại $x=5$ trên khoảng $\left( 0;+\infty \right)$.
(Đúng) Giá trị lớn nhất là 502 trên $\left( 0;5 \right]$.

(Vì): Hàm số đạt giá trị $f(1)=502$ tại $x=1 \in (0;5]$.
(Đúng) Hàm số không có giá trị lớn nhất trên $\left( 0;+\infty \right)$.

(Vì): Trên khoảng $\left( 0;+\infty \right)$, hàm số không có giá trị lớn nhất vì $\lim_{x \to 0^+ }f(x)=+\infty$.