Tại một xí nghiệp chuyên sản xuất vật liệu xây dựng, nếu trong một ngày xí nghiệp sản xuất $x\left( {{\text{m}}^{3}} \right)$ sản phẩm thì phải bỏ ra các khoản chi phí bao gồm

Tại một xí nghiệp chuyên sản xuất vật liệu xây dựng, nếu trong một ngày xí nghiệp sản xuất $x\left( {{\text{m}}^{3}} \right)$ sản phẩm thì phải bỏ ra các khoản chi phí bao gồm: $4$ triệu đồng chi phí cố định; $0,2$ triệu đồng chi phí cho mỗi mét khối sản phẩm và $0,001{{x}^{2}}$ triệu đồng chi phí bảo dưỡng máy móc. Biết rằng, mỗi ngày xí nghiệp sản xuất được tối đa $100{{\text{m}}^{3}}$ sản phẩm. Gọi $C\left( x \right)$ là tổng chi phí để xí nghiệp sản xuất $x\left( {{\text{m}}^{3}} \right)$ sản phẩm trong một ngày và $\overline{C}$ là chi phí trung bình trên mỗi mét khối sản phẩm.

a) $C=0,2x+0,001{{x}^{2}}$ với $0\le x\le 100$.

b) Tổng chi phí sản xuất $100{{\text{m}}^{3}}$ sản phẩm là $30$ triệu đồng.

c) $\overline{C}=0,001x+\dfrac{2}{x}+0,2$ với $0\le x\le 100$.

d) $\overline{C}$ có giá trị thấp nhất bằng $0,3$ triệu đồng (kết quả làm tròn ba chữ số thập phân).

Lời giải: (a) Sai: Tổng chi phí (triệu đồng) để xí nghiệp sản xuất $x\left( {{\text{m}}^{3}} \right)$ sản phẩm trong một ngày là:
$C=C\left( x \right)=4+0,2x+0,001{{x}^{2}}$ với $0\le x\le 100$
(b) Đúng: Thay $x=100$ vào hàm $C\left( x \right)$ ta thu được kết quả là $34$ triệu đồng
(c) Đúng: Chi phí trung bình (triệu đồng) trên mỗi mét khối sản phẩm là
$\overline{C}=\overline{C}\left( x \right)=\dfrac{C\left( x \right)}{x}=\dfrac{4+0,2x+0,001{{x}^{2}}}{x}=0,001x+\dfrac{4}{x}+0,2$ với $0\le x\le 100$
(d) Đúng: Ta có $\overline{C}’\left( x \right)=0,001-\dfrac{4}{{{x}^{2}}}=0\Leftrightarrow 0,001-\dfrac{4}{{{x}^{2}}}=0\Leftrightarrow {{x}^{2}}=4000\Leftrightarrow x=20\sqrt{10}\in \left( 0;100 \right]$
$\overline{C}\left( 20\sqrt{10} \right)=\dfrac{\sqrt{10}}{25}+\dfrac{1}{5}\approx 0,326$
Bảng biến thiên

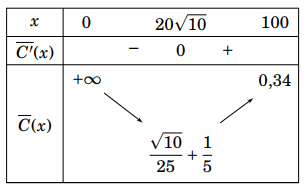
Từ bảng biến thiên, ta thấy chi phí trung bình thấp nhất là $\overline{C}\left( 20\sqrt{10} \right)\approx 0,326$ (triệu đồng/ ${{\text{m}}^{3}}$
sản phẩm), đạt được khi $x=20\sqrt{10}\approx 63$ ${{\text{m}}^{3}}$.
(Sai) $C=0,2x+0,001{{x}^{2}}$ với $0\le x\le 100$.
(Vì): Tổng chi phí phải bao gồm chi phí cố định là $4$ triệu đồng.
(Sai) Tổng chi phí sản xuất $100{{\text{m}}^{3}}$ sản phẩm là $30$ triệu đồng.
(Vì): Thay $x=100$ vào hàm $C\left( x \right)=4+0,2x+0,001{{x}^{2}}$ ta có $C(100) = 4+0,2(100)+0,001(100)^2 = 4+20+10 = 34$ triệu đồng.
(Sai) $\overline{C}=0,001x+\dfrac{2}{x}+0,2$ với $0\le x\le 100$.
(Vì): Chi phí trung bình $\overline{C}\left( x \right)=\dfrac{C\left( x \right)}{x}=\dfrac{4+0,2x+0,001{{x}^{2}}}{x}=0,001x+\dfrac{4}{x}+0,2$.
(Sai) $\overline{C}$ có giá trị thấp nhất bằng $0,3$ triệu đồng (kết quả làm tròn ba chữ số thập phân).
(Vì): Ta có $\overline{C}’\left( x \right)=0,001-\dfrac{4}{{{x}^{2}}}=0\Leftrightarrow {{x}^{2}}=4000\Leftrightarrow x=20\sqrt{10}$. Khi đó $\overline{C}\left( 20\sqrt{10} \right)=\dfrac{\sqrt{10}}{25}+\dfrac{1}{5}\approx 0,326$.