Các mệnh đề sau đúng hay sai?

a) Các chuyên gia y tế ước tính số người nhiễm virus corona kể từ ngày xuất hiện bệnh nhân đầu tiên đến ngày thứ $t$ là $f\left( t \right)=45{{t}^{2}}-{{t}^{3}}$ với $\left( 0\le t\le 25 \right)$

Các mệnh đề sau đúng hay sai?

a) Các chuyên gia y tế ước tính số người nhiễm virus corona kể từ ngày xuất hiện bệnh nhân đầu tiên đến ngày thứ $t$ là $f\left( t \right)=45{{t}^{2}}-{{t}^{3}}$ với $\left( 0\le t\le 25 \right)$. Nếu coi $f\left( t \right)$ là một hàm xác định trên đoạn $\left[ 0;25 \right]$ thì hàm ${f}’\left( t \right)$ được xem là tốc độ truyền bệnh tại thời điểm $t$. Xác định ngày mà tốc độ truyền bệnh lớn nhất là ngày thứ $10$.

b) Một vật chuyển động theo quy luật $s=\dfrac{1}{3}{{t}^{3}}-{{t}^{2}}+9t$ với $t$ (giây) là khoảng thời gian tính từ lúc vật bắt đầu chuyển động và s (mét) là quãng đường vật đi được trong thời gian đó. Hỏi trong khoảng thời gian 10 giây kể từ lúc bắt đầu chuyển động, vận tốc lớn nhất của vật đạt được bằng $80\left( \text{m/s} \right)$.

c) Một vật chuyển động theo quy luật $s=-\dfrac{1}{2}{{t}^{3}}+6{{t}^{2}}$ với $t$ (giây)là khoảng thời gian từ khi vật bắt đầu chuyển động và $s$ (mét) là quãng đường vật di chuyển trong thời gian đó. Hỏi trong khoảng thời gian $6$ giây, kể từ lúc bắt đầu chuyển động, vận tốc lớn nhất vật đạt được bằng $28\left( \text{m/s} \right)$.

d) Một vật chuyển động theo quy luật $s=-\dfrac{1}{3}{{t}^{3}}+6{{t}^{2}}$ với $t$ (giây) là khoảng thời gian tính từ khi vật bắt đầu chuyển động và $s$ (mét) là quãng đường vật di chuyển được trong khoảng thời gian đó. Hỏi trong khoảng thời gian 7 giây, kể từ khi bắt đầu chuyển động, vận tốc lớn nhất của vật đạt được bằng $36\left( \text{m/s} \right)$.

Lời giải:
(a) Từ giả thiết suy ra tốc độ truyền bệnh tại thời điểm $t$ là: ${f}’\left( t \right)=90t-3{{t}^{2}}$.
Xét hàm ${f}’\left( t \right)=90t-3{{t}^{2}}$ với $0\le t\le 25$.
Ta có: ${{f}’}’\left( t \right)=90-6t=0\Leftrightarrow t=15$.
Bảng biến thiên:

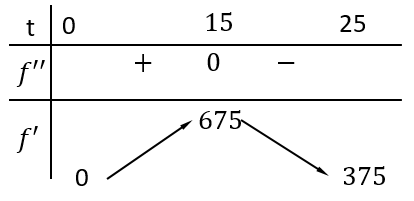
Từ bảng biến thiên ta có ngày mà tốc độ truyền bệnh lớn nhất là ngày thứ $15$.
(b) Theo ý nghĩa vật lí của đạo hàm, vận tốc tức thời của một vật khi chuyển động là đạo hàm của quãng đường theo thời gian $t$.
Vận tốc tức thời của vật tại thời điểm $t$ là $v(t)={s}'(t)={{\left( \dfrac{1}{3}{{t}^{3}}-{{t}^{2}}+9t \right)}^{\prime }}={{t}^{2}}-2t+9$.
Xét hàm số $v\left( t \right)={{t}^{2}}-2t+9$ trên đoạn $\left[ 0;10 \right]$.
${v}'(t)=2t-2=0\Leftrightarrow t=1$.
$v(0)=9$, $v(1)=1^2-2(1)+9=8$, $v(10)=10^2-2(10)+9=89$.
Bảng biến thiên:

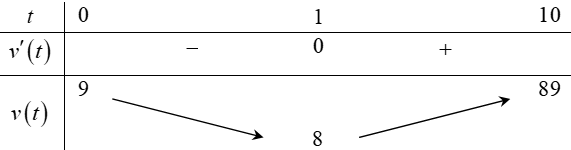
Từ bảng biến thiên giá trị lớn nhất của hàm $v\left( t \right)$ là $89\left( \text{m/s} \right)$.
(c) Ta có $v(t)={s}'(t)={{\left( -\dfrac{1}{2}{{t}^{3}}+6{{t}^{2}} \right)}^{\prime }}=-\dfrac{3}{2}{{t}^{2}}+12t$.
Ta tìm giá trị lớn nhất của $v\left( t \right)$ trên đoạn $\left[ 0;6 \right]$.
${v}'(t)=-3t+12=0\Leftrightarrow t=4$.
Ta tính các giá trị $v(0)=0$, $v(4)=-\dfrac{3}{2}{{\left( 4 \right)}^{2}}+12\left( 4 \right)=-24+48=24$, $v(6)=-\dfrac{3}{2}{{\left( 6 \right)}^{2}}+12\left( 6 \right)=-54+72=18$.
Vậy vận tốc lớn nhất vật đạt được bằng $24\left( \text{m/s} \right)$ tại thời điểm $t=4$ (giây).
(d) Ta có $v\left( t \right)={s}’\left( t \right)={{\left( -\dfrac{1}{3}{{t}^{3}}+6{{t}^{2}} \right)}^{\prime }}=-{{t}^{2}}+12t$.
Ta tìm giá trị lớn nhất của $v\left( t \right)$ trên đoạn $\left[ 0;7 \right]$.
${v}’\left( t \right)=-2t+12=0\Leftrightarrow t=6$.
Khi đó $v\left( 6 \right)=-{{6}^{2}}+12\left( 6 \right)=36$, $v\left( 0 \right)=0$, $v\left( 7 \right)=-{{7}^{2}}+12\left( 7 \right)=-49+84=35$.
Vậy vận tốc lớn nhất đạt được bằng $36\left( \text{m/s} \right)$.
(Sai) Các chuyên gia y tế ước tính số người nhiễm virus corona kể từ ngày xuất hiện bệnh nhân đầu tiên đến ngày thứ $t$ là $f\left( t \right)=45{{t}^{2}}-{{t}^{3}}$ với $\left( 0\le t\le 25 \right)$. Nếu coi $f\left( t \right)$ là một hàm xác định trên đoạn $\left[ 0;25 \right]$ thì hàm ${f}’\left( t \right)$ được xem là tốc độ truyền bệnh tại thời điểm $t$. Xác định ngày mà tốc độ truyền bệnh lớn nhất là ngày thứ $10$.
(Vì): Tốc độ truyền bệnh là ${f}’\left( t \right)=90t-3{{t}^{2}}$. Ta có ${{f}’}’\left( t \right)=90-6t=0\Leftrightarrow t=15$. Lập bảng biến thiên trên $\left[ 0;25 \right]$ ta thấy ${f}’\left( t \right)$ đạt giá trị lớn nhất tại $t=15$, không phải $t=10$.
(Sai) Một vật chuyển động theo quy luật $s=\dfrac{1}{3}{{t}^{3}}-{{t}^{2}}+9t$ với $t$ (giây) là khoảng thời gian tính từ lúc vật bắt đầu chuyển động và s (mét) là quãng đường vật đi được trong thời gian đó. Hỏi trong khoảng thời gian 10 giây kể từ lúc bắt đầu chuyển động, vận tốc lớn nhất của vật đạt được bằng $80\left( \text{m/s} \right)$.
(Vì): Vận tốc tức thời là $v(t)={s}'(t)={{t}^{2}}-2t+9$. Xét trên đoạn $\left[ 0;10 \right]$, ta có $v(0)=9$, $v(1)=8$, $v(10)=10^2-2(10)+9=100-20+9=89$. Giá trị lớn nhất của vận tốc đạt được là $89\left( \text{m/s} \right)$, không phải $80\left( \text{m/s} \right)$.
(Sai) Một vật chuyển động theo quy luật $s=-\dfrac{1}{2}{{t}^{3}}+6{{t}^{2}}$ với $t$ (giây)là khoảng thời gian từ khi vật bắt đầu chuyển động và $s$ (mét) là quãng đường vật di chuyển trong thời gian đó. Hỏi trong khoảng thời gian $6$ giây, kể từ lúc bắt đầu chuyển động, vận tốc lớn nhất vật đạt được bằng $28\left( \text{m/s} \right)$.
(Vì): Vận tốc tức thời là $v(t)={s}'(t)=-\dfrac{3}{2}{{t}^{2}}+12t$. Xét trên đoạn $\left[ 0;6 \right]$, ta có $v'(t)=-3t+12=0 \Leftrightarrow t=4$. Giá trị $v(0)=0$, $v(4)=24$, $v(6)=18$. Vậy vận tốc lớn nhất vật đạt được là $24\left( \text{m/s} \right)$, không phải $28\left( \text{m/s} \right)$.
(Đúng) Một vật chuyển động theo quy luật $s=-\dfrac{1}{3}{{t}^{3}}+6{{t}^{2}}$ với $t$ (giây) là khoảng thời gian tính từ khi vật bắt đầu chuyển động và $s$ (mét) là quãng đường vật di chuyển được trong khoảng thời gian đó. Hỏi trong khoảng thời gian 7 giây, kể từ khi bắt đầu chuyển động, vận tốc lớn nhất của vật đạt được bằng $36\left( \text{m/s} \right)$.
(Vì): Vận tốc tức thời là $v\left( t \right)={s}’\left( t \right)=-{{t}^{2}}+12t$. Xét trên đoạn $\left[ 0;7 \right]$. Ta có ${v}’\left( t \right)=-2t+12=0\Leftrightarrow t=6$. Khi đó $v\left( 6 \right)=-6^2+12(6)=36$, $v\left( 0 \right)=0$, $v\left( 7 \right)=-7^2+12(7)= -49+84=35$. Vậy vận tốc lớn nhất đạt được bằng $36\left( \text{m/s} \right)$.