Một chất điểm chuyển động theo phương trình $s\left( t \right)={{t}^{3}}-3{{t}^{2}}+8t+1$, trong đó $t$ tính bằng giây và $s\left( t \right)$ tính bằng mét

Một chất điểm chuyển động theo phương trình $s\left( t \right)={{t}^{3}}-3{{t}^{2}}+8t+1$, trong đó $t$ tính bằng giây và $s\left( t \right)$ tính bằng mét. Các phát biểu sau đúng hay sai

a) Vận tốc của chất điểm tại thời điểm $t=3\left( s \right)$ bằng $17m/s$.

b) Gia tốc tại thời điểm chất điểm đạt vận tốc nhỏ nhất bằng $2m/{{s}^{2}}$.

c) Tại thời điểm mà chất điểm di chuyển được $13m$, vận tốc khi đó bằng $8m/s$.

d) Vận tốc nhỏ nhất của chất điểm là $5m/s$.

Lời giải: Vận tốc $v\left( t \right)=3{{t}^{2}}-6t+8$
Vận tốc của chất điểm tại thời điểm $t=3\left( s \right)$ bằng $v\left( 3 \right)=17m/s$ Chất điểm di chuyển được $13m$ $\Leftrightarrow {{t}^{3}}-3{{t}^{2}}+8t+1=13\Leftrightarrow t=2\left( s \right)$
Vận tốc khi đó bằng $v\left( 2 \right)=8m/s$.Vận tốc $v\left( t \right)=3{{t}^{2}}-6t+8$
$v’\left( t \right)=6t-6\Leftrightarrow t=1$
Bảng biến thiên

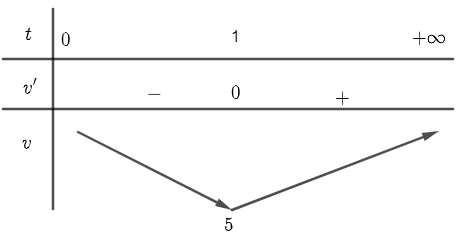
Vận tốc nhỏ nhất bằng $5m/s$ tại thời điểm $t=1\left( s \right)$.Gia tốc $a\left( t \right)=6t-6$
Gia tốc tại thời điểm $t=1\left( s \right)$ bằng $a\left( 1 \right)=0$.
(Đúng) Vận tốc của chất điểm tại thời điểm $t=3\left( s \right)$ bằng $17m/s$.
(Vì): Vận tốc $v\left( t \right)=3{{t}^{2}}-6t+8$
Vận tốc của chất điểm tại thời điểm $t=3\left( s \right)$ bằng $v\left( 3 \right)=17m/s$ Chất điểm di chuyển được $13m$ $\Leftrightarrow {{t}^{3}}-3{{t}^{2}}+8t+1=13\Leftrightarrow t=2\left( s \right)$
Vận tốc khi đó bằng $v\left( 2 \right)=8m/s$.Vận tốc $v\left( t \right)=3{{t}^{2}}-6t+8$
$v’\left( t \right)=6t-6\Leftrightarrow t=1$
Bảng biến thiên

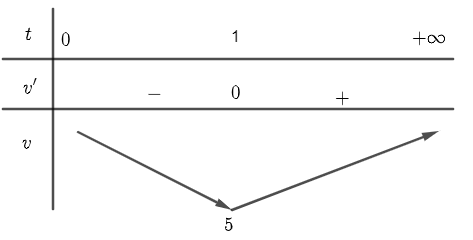
Vận tốc nhỏ nhất bằng $5m/s$ tại thời điểm $t=1\left( s \right)$.Gia tốc $a\left( t \right)=6t-6$
Gia tốc tại thời điểm $t=1\left( s \right)$ bằng $a\left( 1 \right)=0$.
(Đúng) Gia tốc tại thời điểm chất điểm đạt vận tốc nhỏ nhất bằng $2m/{{s}^{2}}$.
(Vì): Vận tốc $v\left( t \right)=3{{t}^{2}}-6t+8$
Vận tốc của chất điểm tại thời điểm $t=3\left( s \right)$ bằng $v\left( 3 \right)=17m/s$ Chất điểm di chuyển được $13m$ $\Leftrightarrow {{t}^{3}}-3{{t}^{2}}+8t+1=13\Leftrightarrow t=2\left( s \right)$
Vận tốc khi đó bằng $v\left( 2 \right)=8m/s$.Vận tốc $v\left( t \right)=3{{t}^{2}}-6t+8$
$v’\left( t \right)=6t-6\Leftrightarrow t=1$
Bảng biến thiên

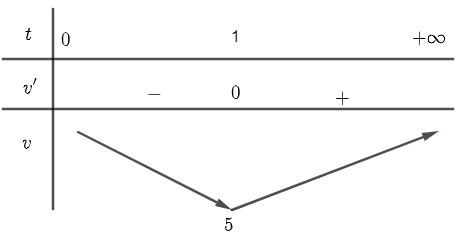
Vận tốc nhỏ nhất bằng $5m/s$ tại thời điểm $t=1\left( s \right)$.Gia tốc $a\left( t \right)=6t-6$
Gia tốc tại thời điểm $t=1\left( s \right)$ bằng $a\left( 1 \right)=0$.
(Đúng) Tại thời điểm mà chất điểm di chuyển được $13m$, vận tốc khi đó bằng $8m/s$.
(Vì): Vận tốc $v\left( t \right)=3{{t}^{2}}-6t+8$
Vận tốc của chất điểm tại thời điểm $t=3\left( s \right)$ bằng $v\left( 3 \right)=17m/s$ Chất điểm di chuyển được $13m$ $\Leftrightarrow {{t}^{3}}-3{{t}^{2}}+8t+1=13\Leftrightarrow t=2\left( s \right)$
Vận tốc khi đó bằng $v\left( 2 \right)=8m/s$.Vận tốc $v\left( t \right)=3{{t}^{2}}-6t+8$
$v’\left( t \right)=6t-6\Leftrightarrow t=1$
Bảng biến thiên

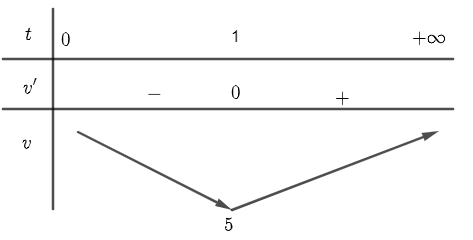
Vận tốc nhỏ nhất bằng $5m/s$ tại thời điểm $t=1\left( s \right)$.Gia tốc $a\left( t \right)=6t-6$
Gia tốc tại thời điểm $t=1\left( s \right)$ bằng $a\left( 1 \right)=0$.
(Đúng) Vận tốc nhỏ nhất của chất điểm là $5m/s$.
(Vì): Vận tốc $v\left( t \right)=3{{t}^{2}}-6t+8$
Vận tốc của chất điểm tại thời điểm $t=3\left( s \right)$ bằng $v\left( 3 \right)=17m/s$ Chất điểm di chuyển được $13m$ $\Leftrightarrow {{t}^{3}}-3{{t}^{2}}+8t+1=13\Leftrightarrow t=2\left( s \right)$
Vận tốc khi đó bằng $v\left( 2 \right)=8m/s$.Vận tốc $v\left( t \right)=3{{t}^{2}}-6t+8$
$v’\left( t \right)=6t-6\Leftrightarrow t=1$
Bảng biến thiên

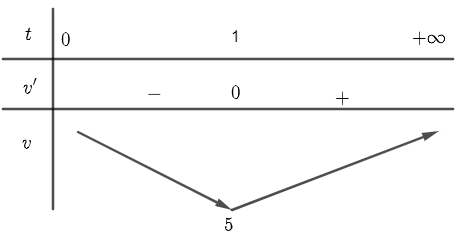
Vận tốc nhỏ nhất bằng $5m/s$ tại thời điểm $t=1\left( s \right)$.Gia tốc $a\left( t \right)=6t-6$
Gia tốc tại thời điểm $t=1\left( s \right)$ bằng $a\left( 1 \right)=0$.