Một quả trứng khủng long đồ chơi bằng nhựa có thiết diện qua trục lớn là một đường elip. Biết độ dài mỗi trục là 12 cm và 8 cm

Bài toán: Một quả trứng khủng long đồ chơi bằng nhựa có thiết diện qua trục lớn là một đường elip. Biết độ dài mỗi trục là 12 cm và 8 cm . Bên trong quả trứng người ta cần thiết kế một chiếc hộp hình trụ để đựng các đồ chơi trẻ con như bóng đèn xanh

đỏ, kẹo v.v… Hỏi khối trụ như thế có thể tích tối đa bao nhiêu $\mathrm{\,c}\mathrm{\,m}^{3}$ (làm tròn đến hàng đơn vị). Lòi giải: Gắn elip lên hệ trục tọa độ $Oxy$ như hình vẽ, elip có $2a=12\Rightarrow a=6;2b=8\Rightarrow b=4$. Phương trình chính tắc elip $\left(E\right):\dfrac{x^{2}}{36}+\dfrac{y^{2}}{16}=1$. 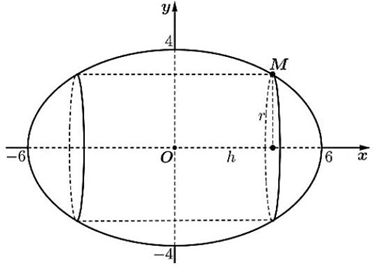Đặt chiều cao và bán kính đáy hình trụ nội tiếp elip là $h,r$ thì điểm tiếp xúc $M\left(\dfrac{h}{2};r\right)$ với $0 $\Rightarrow \dfrac{h^{2}}{144}+\dfrac{r^{2}}{16}=1\Rightarrow r^{2}=16\left(1-\dfrac{h^{2}}{144}\right)$. Thể tích khối trụ là $V=\pi r^{2}h=\pi 16\left(1-\dfrac{h^{2}}{144}\right)\cdot h=\pi \left(16h-\dfrac{h^{3}}{9}\right)$ hay $V=\pi \left(16h-\dfrac{h^{3}}{9}\right)$. Ta có $V’=\pi \left(16-\dfrac{h^{2}}{3}\right);V’=0\Rightarrow 16-\dfrac{h^{2}}{3}=0\Rightarrow h^{2}=48\Rightarrow h=4\sqrt {3} \in \left(0;12\right)$. Giá trị lớn nhất của thể tích khối trụ là $V_{\mathrm{\,max}}=V\left(4\sqrt {3} \right)=\pi \left(16\cdot 4\sqrt {3} -\dfrac{(4\sqrt {3} )^{3}}{9}\right)\approx 232\mathrm{\,\;c}\mathrm{\,m}^{3}$