Hoạ sĩ thiết kế một micro có dạng khối tròn xoay, mặt cắt đứng chứa trục của khối tròn xoay có dạng như hình sau, trong đó $OA=OB=OI=2\mathrm{\,\;cm},MC=MD=1\mathrm{\,\;cm}$, đường thẳng $OM$ là đường trung trực của đoạn thẳng $CD,OM=20\mathrm{\,\;cm},AOB=90^{\circ }$.

Bài toán: Hoạ sĩ thiết kế một micro có dạng khối tròn xoay, mặt cắt đứng chứa trục của khối tròn xoay có dạng như hình sau, trong đó $OA=OB=OI=2\mathrm{\,\;cm},MC=MD=1\mathrm{\,\;cm}$, đường thẳng $OM$ là đường trung trực của đoạn thẳng $CD,OM=20\mathrm{\,\;cm},AOB=90^{\circ }$.

Thể tích của micro này là bao nhiêu $\mathrm{\,c}\mathrm{\,m}^{3}$ ? (Làm tròn kết quả đến hàng đơn vị)

Lòi giải

Trả lòi: 117.

Đặt hệ trục $Oxy$ như hình vẽ, đơn vị của mỗi trục là 1 cm . Gọi $y=f\left(x\right)$ là đồ thị bao gồm cung nhỏ $KA$ và đoạn thẳng $AC$, trong đó

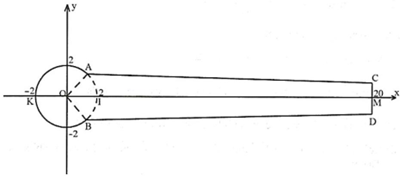
Vì $A\left(\sqrt {2} ;\sqrt {2} \right),C\left(20;1\right)$ nên phương trình đường thẳng $AC$ là

        $\dfrac{x-20}{\sqrt {2} -20}=\dfrac{y-1}{\sqrt {2} -1}\Leftrightarrow y-1=\left(\sqrt {2} -1\right)\dfrac{x-20}{\sqrt {2} -20}\Leftrightarrow y=\dfrac{\left(1-\sqrt {2} \right)x+19\sqrt {2} }{20-\sqrt {2} }$

Phương trình đường tròn là $x^{2}+y^{2}=4$, hàm số có đồ thị cung nhỏ $KA$ là