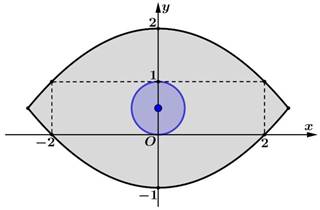
Bài toán: Bạn An thực hiện thiết kế một logo hình con mắt cho một phòng khám nhãn khoa. Logo là một hình phẳng giới hạn bởi hai parabol $y=f\left(x\right)$ và $y=g\left(x\right)$ có các kích thước như hình vẽ dưới đây (phần được tô màu đen) và một hình tròn có bán kính bằng $0,5\mathrm{\,dm}$ ở giữa là phần con ngươi (phần được tô màu xanh), đơn vị trên mỗi trục tọa độ là decimet.

Biết rằng chi phí để sơn phần con ngươi hình tròn màu xanh là 25000 đồng và chi phí để sơn phần còn lại màu đen là 20000 đồng/dm². Chi phí để sơn logo trên là bao nhiêu nghìn đồng? (Kết quả làm tròn đến hàng đơn vị)
Lòi giải
Gọi phương trình parabol $y=f\left(x\right)$ là $f\left(x\right)=ax^{2}+bx+c$ với $a\neq 0$ đi qua các điểm có tọa độ lần lượt là $\left(2;1\right),\left(0;2\right),\left(-2;1\right)$.
Lập hệ phương trình ba ẩn, từ đó suy ra được $\left\{\begin{array}{*{20}{l}}a=-\dfrac{1}{4}\\b=0\\c=2\end{array}\right. $ nên $f\left(x\right)=-\dfrac{1}{4}x^{2}+2$
Gọi phương trình parabol $y=g\left(x\right)$ là $g\left(x\right)=mx^{2}+nx+p$ với $m\neq 0$ đi qua các điểm có tọa độ lần lượt là $\left(-2;0\right),\left(0;-1\right),\left(2;0\right)$.
Lập hệ phương trình ba ẩn, từ đó suy ra được $\left\{\begin{array}{*{20}{l}}m=\dfrac{1}{4}\\n=0\\p=-1\end{array}\right. $ nên $g\left(x\right)=\dfrac{1}{4}x^{2}-1$
Phương trình hoành độ giao điểm: $f\left(x\right)=g\left(x\right)\Leftrightarrow -\dfrac{1}{4}x^{2}+2=\dfrac{1}{4}x^{2}-1\Leftrightarrow \dfrac{1}{2}x^{2}=3\Leftrightarrow x=\pm \sqrt {6} $
Diện tích hình tròn được sơn màu xanh là: $S_{1}=\pi r^{2}=\pi (0,5)^{2}=0,25\pi \left(\mathrm{\,d}\mathrm{\,m}^{2}\right)$
Diện tích hình phẳng giới hạn bởi hai đường thẳng $y=f\left(x\right)$ và $y=g\left(x\right)$ là:
Diện tích phần sơn được tô màu đen là:
Chi phí để sơn logo là:
$T=0,25\pi \cdot 25000+\left( \left. \mathop{\int }_{-\sqrt{6}}^{\sqrt{6}}\left( -\frac{1}{4}{{x}^{2}}+2 \right)-\left( \frac{1}{4}{{x}^{2}}-1 \right) \right|\text{ }\!\!~\!\!\text{ d}x-0,25\pi \right)\cdot 20\cdot 000=200\text{ }\!\!~\!\!\text{ ngh }\!\!\grave{\mathrm{i}}\!\!\text{ n }\!\!~\!\!\text{ }\text{ng}\text{. }\!\!~\!\!\text{ }$
