Tổng số tam giác của hình bên dưới là bao nhiêu?

ĐỀ BÀI:

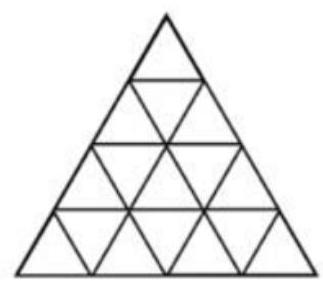
Tổng số tam giác của hình bên dưới là bao nhiêu?

LỜI GIẢI

ĐÁP ÁN 27

Số tam giác có cạnh 4 đơn vị là 1.Số tam giác có cạnh 3 đơn vị là 3.Số tam giác có cạnh 2 đơn vị là 7.Số tam giác có cạnh 1 đơn vị là 16.Tổng có tất cả $1+3+7+16=27$ tam giác.