Khi di chuyển, một vận động viên đua xe motor thường chịu tác động của 4 lực: Trọng lực $\overrightarrow{P}$, phản lực của trọng lực $\overrightarrow{N}$, lực cản của không khí $\overrightarrow{{{F}_{C}}}$ và lực đẩy của động cơ $\overrightarrow{{{F}_{}}}$. Lực cản của không khí ngược hướng với lực đẩy của động cơ và có độ lớn tỉ lệ thuận với bình phương vận tốc xe. Một vận động viên đua xe tăng vận tốc từ $250$ (km/h) lên $300$ (km/h), trong quá trình tăng tốc, xe giữ nguyên hướng di chuyển.

ĐỀ BÀI

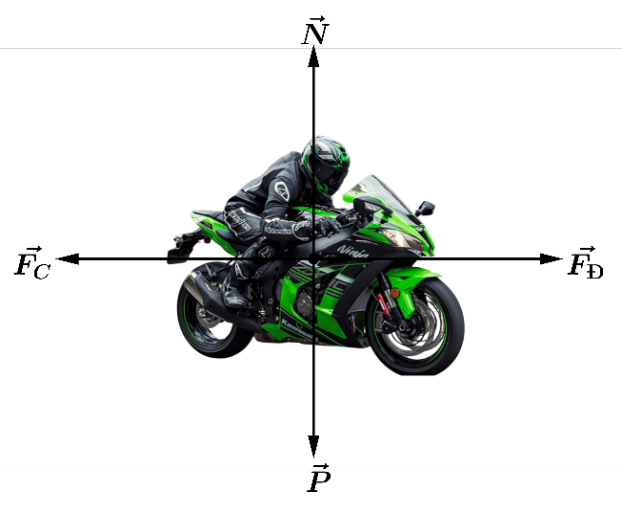
Khi di chuyển, một vận động viên đua xe motor thường chịu tác động của 4 lực: Trọng lực $\overrightarrow{P}$, phản lực của trọng lực $\overrightarrow{N}$, lực cản của không khí $\overrightarrow{{{F}_{C}}}$ và lực đẩy của động cơ $\overrightarrow{{{F}_{}}}$. Lực cản của không khí ngược hướng với lực đẩy của động cơ và có độ lớn tỉ lệ thuận với bình phương vận tốc xe. Một vận động viên đua xe tăng vận tốc từ $250$ (km/h) lên $300$ (km/h), trong quá trình tăng tốc, xe giữ nguyên hướng di chuyển.
Lực cản của không khí khi xe đạt vận tốc $250$ (km/h) lên $300$ (km/h) lần lượt biểu diễn bởi hai vectơ $\overrightarrow{{{F}_{1}}}$ và $\overrightarrow{{{F}_{2}}}$ với $\overrightarrow{{{F}_{1}}}+\dfrac{a}{b}.\overrightarrow{{{F}_{2}}}=\overrightarrow{0}\left( a\in \mathbb{Z},b\in \mathbb{N}* \right)$. Tính giá trị của biểu thức $T=a+b$.

LỜI GIẢI

ĐÁP ÁN 11

Vì trong quá trình vận động viên tăng vận tốc từ $250$ (km/h) lên $300$ (km/h), xe giữ nguyên hướng di chuyển nên hai vectơ $\overrightarrow{{{F}_{1}}}$ và $\overrightarrow{{{F}_{2}}}$ có cùng hướng và $\overrightarrow{{{F}_{1}}}+\dfrac{a}{b}\overrightarrow{{{F}_{2}}}=\overrightarrow{0}$ $\left( a\in \mathbb{Z},b\in \mathbb{N}* \right)$.Vì lực cản của không khí ngược hướng với lực đẩy của động cơ và có độ lớn tỉ lệ thuận với bình phương vận tốc xe motor nên $\left| \dfrac{\overrightarrow{{{F}_{1}}}}{\overrightarrow{{{F}_{2}}}} \right|=\dfrac{{{250}^{2}}}{{{300}^{2}}}=\dfrac{25}{36}\Rightarrow \left| \overrightarrow{{{F}_{1}}} \right|=\dfrac{25}{36}\left| \overrightarrow{{{F}_{2}}} \right|\Rightarrow \overrightarrow{{{F}_{1}}}=\dfrac{25}{36}\overrightarrow{{{F}_{2}}}\Rightarrow \overrightarrow{{{F}_{1}}}-\dfrac{25}{36}\overrightarrow{{{F}_{2}}}=\overrightarrow{0}$.Vậy $\dfrac{a}{b}=\dfrac{-25}{36}\Rightarrow a+b=11$.