Giải SBT Bài 9: Tính chất ba đường phân giác của tam giác (C8 SBT Toán 7 Chân trời)
========
Giải bài 1 trang 65 SBT Toán 7 Chân trời sáng tạo tập 2 – CTST
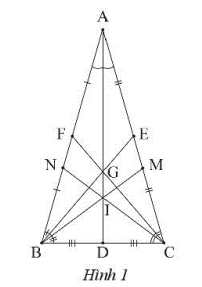
Cho tam giác ABC cân tại A. Gọi G là trọng tâm của tam giác và gọi I là giao điểm của các đường phân giác của tam giác. Chứng minh ba điểm A, I, G thẳng hàng.
Hướng dẫn giải chi tiết Bài 1
Phương pháp giải
Chứng minh AD vừa là trung tuyến vừa là phân giác của tam giác ABC cân tại A
Lời giải chi tiết

Vé phân giác AD của tam giác ABC.
Ta có tam giác ABC cân tại A nên AD vừa là phân giác vừa là trung tuyến suy ra hai điểm I và G đều thuộc AD, suy ra ba điểm A, I, G thẳng hàng.
–>
— *****
Giải bài 2 trang 65 SBT Toán 7 Chân trời sáng tạo tập 2 – CTST
Cho tam giác ABC có \(\widehat {{A^{}}} = {42^o}\), ba đường phân giác đồng quy tại I. Tính số đo góc BIC.
Hướng dẫn giải chi tiết Bài 2
Phương pháp giải
Sử dụng tính chất tia phân giác của một góc để tính số đo góc.
Lời giải chi tiết
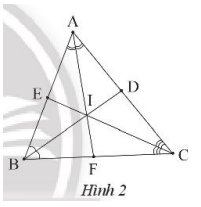
Ta có: \(\widehat B + \widehat C = {180^o} – \widehat {{A^{}}} = {180^o} – {62^o} = {118^o}\)
Do BI và CI là phân giác của góc B và góc C của tam giác ABC nên:
\(\widehat {IBC} + \widehat {ICB} = \frac{{\widehat B + \widehat C}}{2} = \frac{{{{118}^o}}}{2} = {59^o}\)
Suy ra: \(\widehat {BIC} = {180^o} – \left( {\widehat {IBC} + \widehat {ICB}} \right) = {180^o} – {59^o} = {121^o}\)
–>
— *****
Giải bài 3 trang 65 SBT Toán 7 Chân trời sáng tạo tập 2 – CTST
Cho tam giác ABC cân tại A. Vẽ đường phân giác AD. Gọi H và K là chân các đường vuông góc kẻ từ D đến AB và AC. Chứng minh rằng DH = DK.
Hướng dẫn giải chi tiết Bài 3
Phương pháp giải
Chứng minh: \(\Delta A{\rm{D}}H = \Delta A{\rm{D}}K\)
Lời giải chi tiết
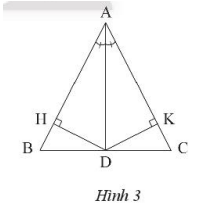
Xét hai tam giác vuông ADH và ADK có:
cạnh huyền AD chung
\(\widehat {BA{\rm{D}}} = \widehat {CA{\rm{D}}}\) ( vì AD là phân giác của góc A)
Suy ra: \(\Delta A{\rm{D}}H = \Delta A{\rm{D}}K\) (cạnh huyền – góc nhọn)
Suy ra: DH = DK
–>
— *****
Giải bài 4 trang 65 SBT Toán 7 Chân trời sáng tạo tập 2 – CTST
Cho tam giác ABC có đường trung tuyến AM đồng thời là đường phân giác. Chứng minh tam giác ABC là tam giác cân.
Hướng dẫn giải chi tiết Bài 4
Phương pháp giải
Chứng minh: \(\Delta BMH = \Delta CMK\) suy ra \(\widehat B = \widehat C\)
Lời giải chi tiết
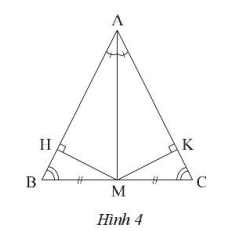
Gọi H và K là chân đường vuông góc kẻ từ M đến AB và AC.
Do AM là tia phân giác của góc BAC nên MH = MK
Xét hai tam giác vuông BMH và CMK có:
Cạnh huyền BM = CM
Cạnh góc vuông: MH = MK
Suy ra: \(\Delta BMH = \Delta CMK\) (cạnh huyền – cạnh góc vuông)
Suy ra: \(\widehat B = \widehat C\)
Vậy tam giác ABC cân tại A.
–>
— *****
