Bài toán gốc
Trong một thí nghiệm y học, người ta cấy 1000 vi khuẩn vào môi trường dinh dưỡng. bằng thực nghiệm, người ta xác định được số lượng vi khuẩn thay đổi theo thời gian bởi công thức: $N(t)=1000+\dfrac{100t}{100+{{t}^{2}}}$, trong đó $t$ là thời gian tính bằng giây. Hỏi thời gian bằng bao nhiêu để số lượng vi khuẩn đạt cực đại?
Đáp án: 10
Lời giải: Ta có ${N}’\left( t \right)=\dfrac{100\left( 100-{{t}^{2}} \right)}{{{\left( 100+{{t}^{2}} \right)}^{2}}}=0\Leftrightarrow 100-{{t}^{2}}=0\Leftrightarrow t=10$.
Bảng biến thiên như sau
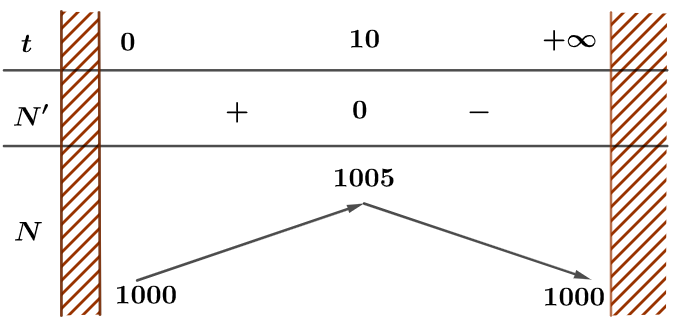
Vậy số lượng vi khuẩn đạt cực đại bằng 1005 khi $t=10$.
Phân tích và Phương pháp giải
Đây là dạng toán ứng dụng đạo hàm để tìm giá trị lớn nhất (cực đại) của hàm số mô tả sự thay đổi của một đại lượng vật lý/sinh học theo thời gian. Phương pháp giải là tính đạo hàm cấp một của hàm số $N(t)$, giải phương trình $N'(t)=0$ để tìm các điểm cực trị, sau đó lập bảng biến thiên (hoặc sử dụng đạo hàm cấp hai) để xác định điểm cực trị nào là cực đại (giá trị lớn nhất).
Bài toán tương tự
Trong một nghiên cứu về sự phát triển của loài côn trùng, số lượng cá thể trong một quần thể được mô tả bởi công thức $P(t)=500+\dfrac{50t}{25+{{t}^{2}}}$, trong đó $t$ là thời gian tính bằng ngày ($t \ge 0$). Hỏi sau bao lâu (tính bằng ngày) thì số lượng cá thể trong quần thể đạt mức tối đa?Đáp án: 5 ngày. Lời giải ngắn gọn: Ta tính đạo hàm $P'(t) = 50 \cdot \dfrac{(25+t^2) – t(2t)}{(25+t^2)^2} = 50 \cdot \dfrac{25 – t^2}{(25+t^2)^2}$. Cho $P'(t) = 0$, ta được $25 – t^2 = 0$. Vì $t \ge 0$, suy ra $t=5$. Lập bảng biến thiên xác nhận $t=5$ là thời điểm số lượng cá thể đạt cực đại.
