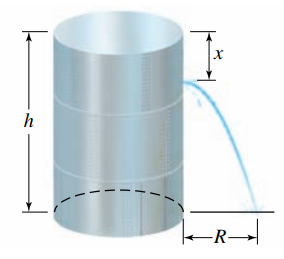
Một bồn hình trụ cao ${h}$ chứa nước. Theo định luật Torricelli, vận tốc tia nước chảy qua lỗ ở độ sâu ${x}$ so với mặt nước là ${V=\sqrt{2 g x}}$. Người ta cho rằng tầm xa ${R}$ (feet) của tia nước được cho bởi $R=2\sqrt{x(h-x)}$
Biết lỗ phun nên đặt ở độ cao $x=K.h,(K\in \mathbb{R})$ so với mặt bồn thì tầm xa ${R}$ đạt cực đại. Tìm $K$ ?
Lời giải
Trả lời: 0,5
Thay vì trực tiếp tối đa ${R(x)}$, ta có thể tối đa ${R^2(x)}$ (vì hàm căn là tăng):
${{R}^{2}}(x)=4x(h-x)=4\left( hx-{{x}^{2}} \right)$
Tính đạo hàm: ${{\left( {{R}^{2}}(x) \right)}^{\prime }}=4(h-2x)$
Giải ${{\left( {{R}^{2}} \right)}^{\prime }}=0$ : $h-2x=0\Rightarrow x=\dfrac{h}{2}.$
Lập bảng biến thiên ta có $x=\dfrac{h}{2}$ là điểm cực đại.
Vậy lỗ phun nên đặt ở độ cao $x=\dfrac{h}{2}$ để tầm xa ${R}$ của tia nước đạt tối đa.
