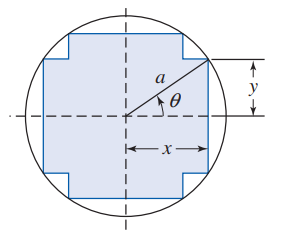
Khi chế tạo một biến áp ${A C}$, một lõi sắt dạng hình chữ thập được đặt vào cuộn dây (xem hình). Giả sử bán kính cuộn là ${a}$. Hỏi góc $\theta$ bằng bao nhiêu độ để tổng diện tích bề mặt lõi sắt là lớn nhất.
Lời giải
Trả lời: 31,7
Đặt ${x=a \cos \theta, y=a \sin \theta}$ suy ra $S=4xy+4y(x-y)=8xy-4{{y}^{2}}=4{{a}^{2}}\left( \sin 2\theta -{{\sin }^{2}}\theta \right)$ trên khoảng ${0 \leq \theta \leq \dfrac{\pi}{4}}$.
Ta có $S(\theta )=4{{a}^{2}}\left( \sin 2\theta -{{\sin }^{2}}\theta \right),\quad 0\le \theta \le \dfrac{\pi }{4}$
Tính đạo hàm ${S^{\prime}(\theta)}$ : ${{S}^{\prime }}(\theta )=4{{a}^{2}}(2\cos 2\theta -\sin 2\theta )$
Giải ${S^{\prime}(\theta)=0}$ : $2\cos 2\theta -\sin 2\theta =0\Rightarrow 2\cos 2\theta =\sin 2\theta \Rightarrow \tan 2\theta =2.$
Vì ${0 \leq 2 \theta \leq \dfrac{\pi}{2}}$, nghiệm duy nhất là $2\theta =\arctan 2\Rightarrow \theta =\dfrac{1}{2}\arctan 2\approx 0,5536rad\left( \approx 31,{{7}^{{}^\circ }} \right)$
Lập bảng biến thiên ta có: tại $\theta \approx 0,5536rad$ là điểm cực đại hay tổng diện tích bề mặt lõi sắt lớn nhất khi $\theta \approx 31,7{}^\circ$
Khi đó:
$\begin{array}{l}
\theta =\dfrac{1}{2}\arctan 2\Rightarrow \cos \theta =\sqrt{\dfrac{1+\cos 2\theta }{2}}=\sqrt{\dfrac{1+\dfrac{1}{\sqrt{5}}}{2}}=\sqrt{\dfrac{\sqrt{5}+1}{2\sqrt{5}}} \\
\sin \theta =\sqrt{\dfrac{1-\cos 2\theta }{2}}=\sqrt{\dfrac{1-\dfrac{1}{\sqrt{5}}}{2}}=\sqrt{\dfrac{\sqrt{5}-1}{2\sqrt{5}}} \\
\end{array}$
Vậy nghiệm tối ưu là $\theta =\dfrac{1}{2}\arctan 2,\quad x=a\sqrt{\dfrac{\sqrt{5}+1}{2\sqrt{5}}},\quad y=a\sqrt{\dfrac{\sqrt{5}-1}{2\sqrt{5}}}.$
