Hai chất điểm $A$ và $B$ chuyển động thẳng đều cùng hướng về $O$ (như hình vẽ), biết rằng vận tốc ${{V}_{B}}=\dfrac{{{V}_{A}}}{\sqrt{3}}$ và góc $\measuredangle AOB={{30}^{0}}$

Hai chất điểm $A$ và $B$ chuyển động thẳng đều cùng hướng về $O$ (như hình vẽ), biết rằng vận tốc ${{V}_{B}}=\dfrac{{{V}_{A}}}{\sqrt{3}}$ và góc $\measuredangle AOB={{30}^{0}}$. Biết rằng khi khoảng cách giữa hai chất điểm $A$ và $B$ là nhỏ nhất thì số đo góc $\widehat{BAO}=\gamma .$ Tìm $\gamma .$

Lời giải

Đáp số: $30.$

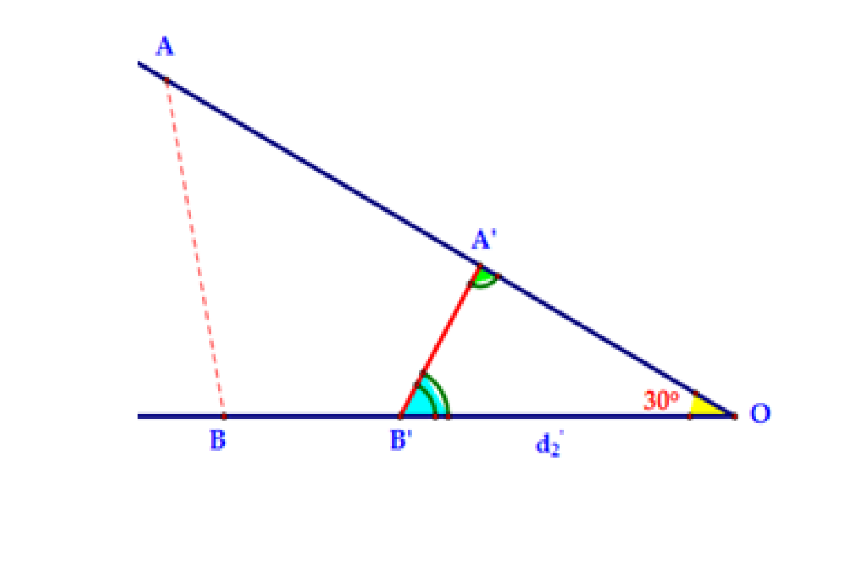
Gọi ${{d}_{1}},{{d}_{2}}$ lần lượt là khoảng cách các vật $A$ và $B$ đến $O$ lúc đầu ( $t=0$ ), đồng thời $d=AB$. Gọi $t’$ là thời điểm mà ${{d}_{\min }}$. Khi đó $A$ ở $A’$ và $B$ ở $B’$ như hình vẽ.

Kí hiệu góc $\measuredangle B’A’O=\beta ,\measuredangle A’B’O=\gamma$.

Áp dụng định lý sin trong tam giác $\Delta A’B’O$ ta có:

$\dfrac{d}{\operatorname{s}\text{in}30}=\dfrac{OA’}{\sin \gamma }=\dfrac{OB’}{\sin \beta }\Leftrightarrow 2d=\dfrac{{{d}_{1}}-AA’}{\sin \gamma }=\dfrac{{{d}_{2}}-BB’}{\sin \beta }\Leftrightarrow 2d=\dfrac{{{d}_{1}}-{{v}_{1}}t}{\sin \gamma }=\dfrac{{{d}_{2}}-{{v}_{2}}t}{\sin \beta }\left( * \right)$

Do ${{v}_{2}}=\dfrac{{{v}_{1}}}{\sqrt{3}}$ và áp dụng $\dfrac{A}{B}=\dfrac{C}{D}=\dfrac{C-A}{D-B}$, ta có:

$\left( * \right)\Leftrightarrow 2d=\dfrac{\sqrt{3}{{d}_{2}}-{{d}_{1}}}{\sqrt{3}\sin \beta -\sin \gamma }$ mà $\sin \beta =\sin \left( {{180}^{0}}-\beta \right)=\sin \left( {{30}^{0}}+\gamma \right)$

Do đó ta có $d=\dfrac{\sqrt{3}{{d}_{2}}-{{d}_{1}}}{2\left[ \sqrt{3}\sin \left( {{30}^{0}}+\gamma \right)-\sin \gamma \right]}=\dfrac{\sqrt{3}{{d}_{2}}-{{d}_{1}}}{\sqrt{3}\cos \gamma +\sin \gamma }$

Xét $f\left( \gamma \right)=\sqrt{3}\cos \gamma +\sin \gamma$. Ta có ${{d}_{\min }}\Leftrightarrow f{{\left( \gamma \right)}_{\max }}$

$f’\left( \gamma \right)=-\sqrt{3}\sin \gamma +c\text{os}\gamma ;f’\left( \gamma \right)=0\Leftrightarrow -\sqrt{3}\sin \gamma +c\text{os}\gamma =0\Leftrightarrow \tan \gamma =\dfrac{1}{\sqrt{3}}\Leftrightarrow \gamma ={{30}^{0}}.$

$f”\left( \gamma \right)=-\sqrt{3}\text{cos}\gamma -\text{sin}\gamma ;f”\left( {{30}^{0}} \right)=-\sqrt{3}\text{cos}{{30}^{0}}-\text{sin}{{30}^{0}}=-2{<}0$

Vậy, khi $\gamma ={{30}^{0}}$ thì khoảng cách giữa hai chất điểm $A$ và $B$ là nhỏ nhất.