Tính \(\int {\frac{1}{{{x^2} – 4x + 3}}dx} \), kết quả là:

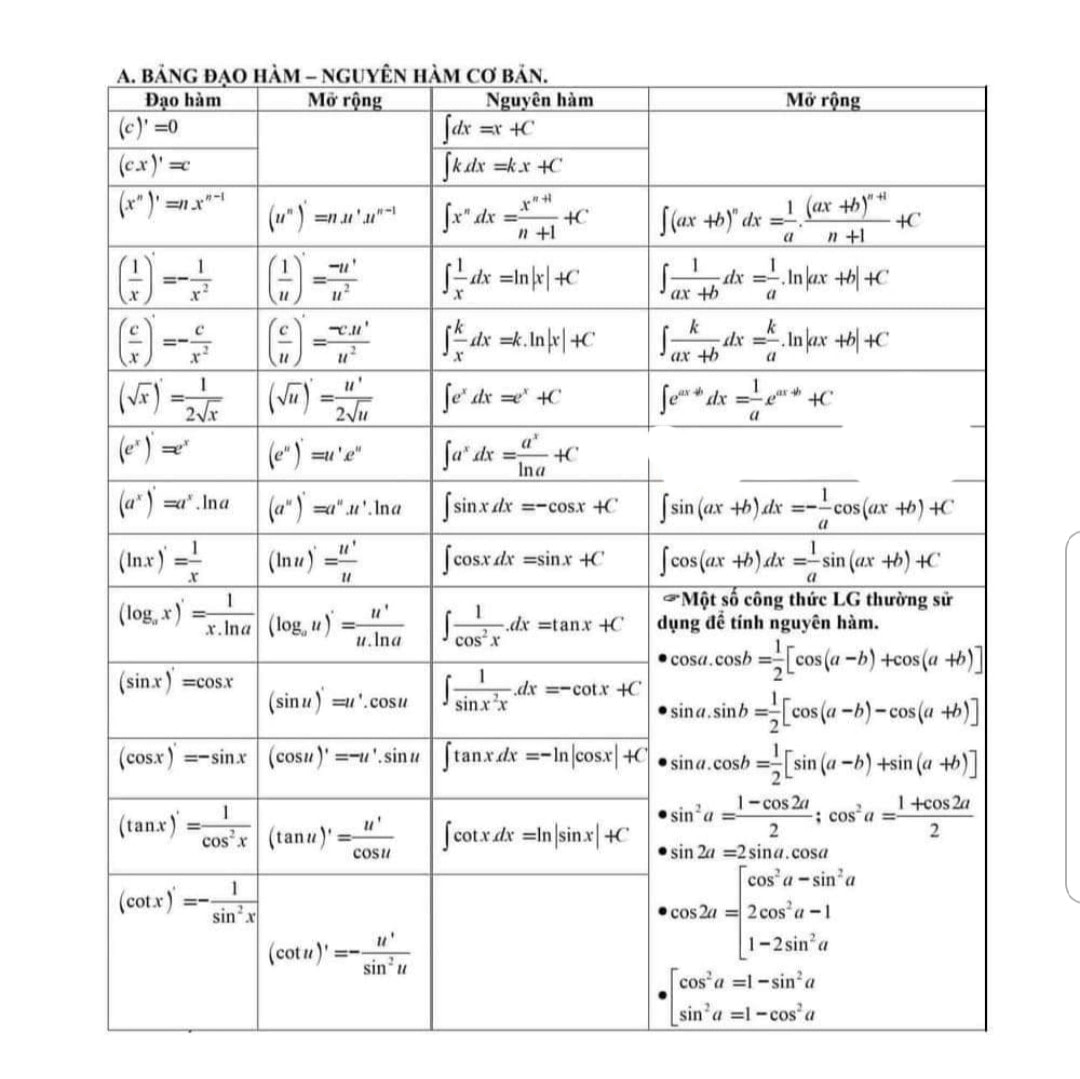
Ta có:

\(\begin{array}{l}
\frac{1}{{{x^2} – 4x + 3}} = \frac{1}{{\left( {x – 1} \right)\left( {x – 3} \right)}}\mathop = \limits^{{\rm{Đặt}}} \frac{A}{{x – 1}} + \frac{B}{{x – 3}}\\
= \frac{{A\left( {x – 3} \right) + B\left( {x – 1} \right)}}{{\left( {x – 1} \right)\left( {x – 3} \right)}}\\
= \frac{{\left( {A + B} \right)x – 3A – B}}{{\left( {x – 1} \right)\left( {x – 3} \right)}}\\
\Rightarrow \left\{ \begin{array}{l}
A + B = 0\\
– 3A – B = 1
\end{array} \right. \Rightarrow \left\{ \begin{array}{l}
A = – \frac{1}{2}\\
B = \frac{1}{2}
\end{array} \right. \Rightarrow \frac{1}{{{x^2} – 4x + 3}} = \frac{1}{{2\left( {x – 3} \right)}} – \frac{1}{{2\left( {x – 1} \right)}}
\end{array}\)

Khi đó:

\(\begin{array}{l}
\int {\frac{1}{{{x^2} – x + 3}}dx} = \frac{1}{2}\int {\left( {\frac{1}{{x – 3}} – \frac{1}{{x – 1}}} \right)dx} \\
= \frac{1}{2}\left( {\ln \left| {x – 3} \right| – \ln \left| {x – 1} \right|} \right) + C\\
= \frac{1}{2}\ln \left| {\frac{{x – 3}}{{x – 1}}} \right| + C
\end{array}\)