Câu hỏi:
Tìm nguyên hàm của hàm số \(f\left( x \right) = {2^x}{.3^{ – 2x}}\)
Lời Giải:
Đây là các câu trắc nghiệm về NGUYÊN HÀM mức độ 1,2 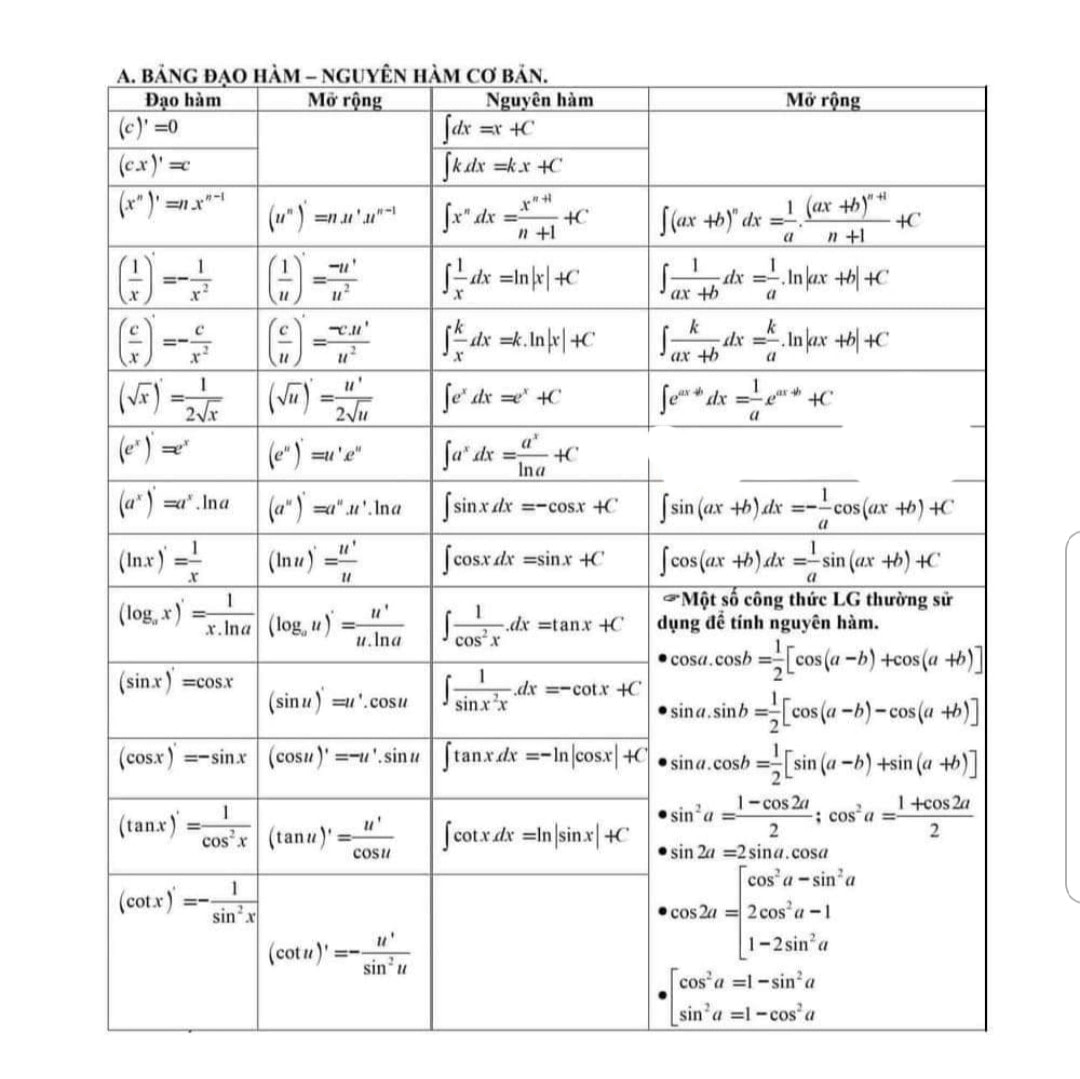
===============
====================
Thuộc chủ đề: Trắc nghiệm Nguyên hàm
Câu hỏi:
Tìm nguyên hàm của hàm số \(f\left( x \right) = {2^x}{.3^{ – 2x}}\)
Lời Giải:
Đây là các câu trắc nghiệm về NGUYÊN HÀM mức độ 1,2 
===============
====================
Thuộc chủ đề: Trắc nghiệm Nguyên hàm
