Câu hỏi: Cho hình chóp \(S.ABCD\) có đáy ABCD là hình thang cân, đáy lớn \(AD=2a,\) \(AB=BC=CD=a.\) Cạnh bên \(SA=2a,\) và vuông góc với đáy. Gọi R bán kính mặt cầu ngoại tiếp khối chóp \(S.ABCD\). Tỉ số \(\frac{R}{a}\) nhận giá trị nào sau đây? A. \(a\sqrt{2}\) B. \(a\) C. \(1\) D. \(\sqrt{2}\) Lời Giải: Đây là các bài toán Mặt cầu trong phần Hình học 12 - … [Đọc thêm...] vềCho hình chóp \(S.ABCD\) có đáy ABCD là hình thang cân, đáy lớn \(AD=2a,\) \(AB=BC=CD=a.\) Cạnh bên \(SA=2a,\) và vuông góc với đáy. Gọi R bán kính mặt cầu ngoại tiếp khối chóp \(S.ABCD\). Tỉ số \(\frac{R}{a}\) nhận giá trị nào sau đây?
Kết quả tìm kiếm cho: ty so
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh bằng \(a.\) Đường thẳng \(SA=a\sqrt{2}\) vuông góc với đáy \(\left( ABCD \right).\) Gọi M trung điểm SC, mặt phẳng \(\left( \alpha \right)\) đi qua hai điểm A và M đồng thời song song với BD cắt \(SB,SD\) lần lượt tại \(E,F.\) Bán kính mặt cầu đi qua năm điểm \(S,A,E,M,F\) nhận giá trị nào sau đây?
Câu hỏi: Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh bằng \(a.\) Đường thẳng \(SA=a\sqrt{2}\) vuông góc với đáy \(\left( ABCD \right).\) Gọi M trung điểm SC, mặt phẳng \(\left( \alpha \right)\) đi qua hai điểm A và M đồng thời song song với BD cắt \(SB,SD\) lần lượt tại \(E,F.\) Bán kính mặt cầu đi qua năm điểm \(S,A,E,M,F\) nhận giá trị nào sau đây? A. … [Đọc thêm...] vềCho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh bằng \(a.\) Đường thẳng \(SA=a\sqrt{2}\) vuông góc với đáy \(\left( ABCD \right).\) Gọi M trung điểm SC, mặt phẳng \(\left( \alpha \right)\) đi qua hai điểm A và M đồng thời song song với BD cắt \(SB,SD\) lần lượt tại \(E,F.\) Bán kính mặt cầu đi qua năm điểm \(S,A,E,M,F\) nhận giá trị nào sau đây?
Đường kính của một khối cầu bằng cạnh của một khối lập phương. Gọi V1 là thể tích khối lập phương, V2 là thể tích khối cầu. Tính tỉ số \( \frac{{{V_1}}}{{{V_2}}}\)
Câu hỏi: Đường kính của một khối cầu bằng cạnh của một khối lập phương. Gọi V1 là thể tích khối lập phương, V2 là thể tích khối cầu. Tính tỉ số \( \frac{{{V_1}}}{{{V_2}}}\) A. \(\pi \) B. \( \frac{1}{\pi }\) C. \( \frac{6}{\pi }\) D. \( \frac{3}{\pi }\) Lời Giải: Đây là các bài toán Mặt cầu trong phần Hình học 12 - PHẦN MẶT TRÒN XOAY . Ta có công … [Đọc thêm...] vềĐường kính của một khối cầu bằng cạnh của một khối lập phương. Gọi V1 là thể tích khối lập phương, V2 là thể tích khối cầu. Tính tỉ số \( \frac{{{V_1}}}{{{V_2}}}\)
Có một hộp nhựa hình lập phương người ta bỏ vào hộp đó 1 quả bóng đá. Tính tỉ số \( \frac{{{V_1}}}{{{V_2}}},\), trong đó V1 là tổng thế tích của quả bóng đá, V2 là thể tích của chiếc hộp đựng bóng. Biết rằng đường tròn lớn trên quả bóng có thể nội tiếp bốn mặt hình vuông của chiếc hộp.
Câu hỏi: Có một hộp nhựa hình lập phương người ta bỏ vào hộp đó 1 quả bóng đá. Tính tỉ số \( \frac{{{V_1}}}{{{V_2}}},\), trong đó V1 là tổng thế tích của quả bóng đá, V2 là thể tích của chiếc hộp đựng bóng. Biết rằng đường tròn lớn trên quả bóng có thể nội tiếp bốn mặt hình vuông của chiếc hộp. A. \( \frac{\pi }{2}.\) B. \( \frac{\pi }{4}.\) C. \( \frac{\pi … [Đọc thêm...] vềCó một hộp nhựa hình lập phương người ta bỏ vào hộp đó 1 quả bóng đá. Tính tỉ số \( \frac{{{V_1}}}{{{V_2}}},\), trong đó V1 là tổng thế tích của quả bóng đá, V2 là thể tích của chiếc hộp đựng bóng. Biết rằng đường tròn lớn trên quả bóng có thể nội tiếp bốn mặt hình vuông của chiếc hộp.
Một nóc tòa nhà cao tầng có dạng hình nón. Người ta muốn xây một bể nước có dạng một hình trụ nội tiếp trong hình nón để chứa nước (như hình vẽ minh họa). Cho biết SO=h;OB=R;OH=x0<x<h. Tìm thể tích lớn nhất của hình trụ.
Câu hỏi: Một nóc tòa nhà cao tầng có dạng hình nón. Người ta muốn xây một bể nước có dạng một hình trụ nội tiếp trong hình nón để chứa nước (như hình vẽ minh họa). Cho biết SO=h;OB=R;OH=x0<x<h. Tìm thể tích lớn nhất của hình trụ. A. \(\frac{{4\pi {R^2}h}}{{27}}\) B. \(\frac{{4\pi {R^2}h}}{{9}}\) C. \(\frac{{2\pi {R^2}h}}{{27}}\) D. \(\frac{{2\pi … [Đọc thêm...] vềMột nóc tòa nhà cao tầng có dạng hình nón. Người ta muốn xây một bể nước có dạng một hình trụ nội tiếp trong hình nón để chứa nước (như hình vẽ minh họa). Cho biết SO=h;OB=R;OH=x0<x<h. Tìm thể tích lớn nhất của hình trụ.
Trong không gian Oxyz, cho mặt cầu \((S):{x^2} + {y^2} + {z^2} – 2x + 4y – 4z – m = 0\) có bán kính R = 5. Giá trị của tham số m bằng
Câu hỏi: Trong không gian Oxyz, cho mặt cầu \((S):{x^2} + {y^2} + {z^2} – 2x + 4y – 4z – m = 0\) có bán kính R = 5. Giá trị của tham số m bằng A. -16 B. 16 C. 4 D. -4 Lời Giải: Đây là các bài toán toạ độ Mặt cầu trong phần Hình học OXYZ. Mặt cầu (S) có tâm \(I\left( {1; – 2;2} \right)\) Ta có \(R = \sqrt {1 + 4 + 4 + m} = 5 \Leftrightarrow m = … [Đọc thêm...] vềTrong không gian Oxyz, cho mặt cầu \((S):{x^2} + {y^2} + {z^2} – 2x + 4y – 4z – m = 0\) có bán kính R = 5. Giá trị của tham số m bằng
Trong không gian với hệ trục Oxyz, cho mặt phẳng \(\left( P \right):2x + 2y + z – {m^2} – 3m = 0\) và mặt cầu \(\left( S \right):{\left( {x – 1} \right)^2} + {\left( {y + 1} \right)^2} + {\left( {z – 1} \right)^2} = 9\). Có bao nhiêu giá trị thực của tham số m để mặt phẳng \(\left( P \right)\) tiếp xúc với mặt cầu \(\left( S \right)\).
Câu hỏi: Trong không gian với hệ trục Oxyz, cho mặt phẳng \(\left( P \right):2x + 2y + z – {m^2} – 3m = 0\) và mặt cầu \(\left( S \right):{\left( {x – 1} \right)^2} + {\left( {y + 1} \right)^2} + {\left( {z – 1} \right)^2} = 9\). Có bao nhiêu giá trị thực của tham số m để mặt phẳng \(\left( P \right)\) tiếp xúc với mặt cầu \(\left( S \right)\). A. 3 B. 1 C. 2 D. … [Đọc thêm...] vềTrong không gian với hệ trục Oxyz, cho mặt phẳng \(\left( P \right):2x + 2y + z – {m^2} – 3m = 0\) và mặt cầu \(\left( S \right):{\left( {x – 1} \right)^2} + {\left( {y + 1} \right)^2} + {\left( {z – 1} \right)^2} = 9\). Có bao nhiêu giá trị thực của tham số m để mặt phẳng \(\left( P \right)\) tiếp xúc với mặt cầu \(\left( S \right)\).
Trong không gian Oxyz, gọi \(\left( S \right)\) là mặt cầu có tâm I thuộc đường thẳng \(\frac{x}{2} = \frac{y}{3} = \frac{{z – 1}}{4}\) và đi qua điểm \(M\left( {0;3;9} \right)\). Biết điểm I có hoành độ là số nguyên và cách đều hai mặt phẳng x – 2y + 2z + 2 = 0, 3x – 2 = 0. Phương trình của \(\left( S \right)\) là:
Câu hỏi: Trong không gian Oxyz, gọi \(\left( S \right)\) là mặt cầu có tâm I thuộc đường thẳng \(\frac{x}{2} = \frac{y}{3} = \frac{{z – 1}}{4}\) và đi qua điểm \(M\left( {0;3;9} \right)\). Biết điểm I có hoành độ là số nguyên và cách đều hai mặt phẳng x – 2y + 2z + 2 = 0, 3x – 2 = 0. Phương trình của \(\left( S \right)\) là: A. \({\left( {x – 6} \right)^2} + {\left( {y – … [Đọc thêm...] vềTrong không gian Oxyz, gọi \(\left( S \right)\) là mặt cầu có tâm I thuộc đường thẳng \(\frac{x}{2} = \frac{y}{3} = \frac{{z – 1}}{4}\) và đi qua điểm \(M\left( {0;3;9} \right)\). Biết điểm I có hoành độ là số nguyên và cách đều hai mặt phẳng x – 2y + 2z + 2 = 0, 3x – 2 = 0. Phương trình của \(\left( S \right)\) là:
Đề thi mẫu HK1 Toán lớp 10 – số 10
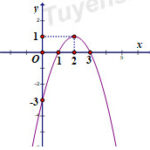
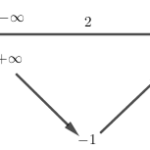
Đề bài Câu 1 : Hàm số nào sau đây có đồ thị như hình bên? A. \(y = - {x^2} + 2x - 3\). B. \(y = - {x^2} + 4x - 3\). C. \(y = {x^2} - 4x + 3\). D. \(y = {x^2} - 2x - 3\). Câu 2 : Bảng biến thiên của hàm số \(y = - 2{x^2} + 4x + 1\) là bảng nào sau đây? Câu 3 : Độ dài các cạnh của một đám vườn hình chữ nhật là \(x = 7,8m \pm … [Đọc thêm...] vềĐề thi mẫu HK1 Toán lớp 10 – số 10
Đề thi mẫu HK1 Toán lớp 10 – số 9
Đề bài Câu 1( 3,5 điểm) Cho hàm số :\(y = {x^2} - 2mx + 3\) 1. Khảo sát sự biến thiên và vẽ đồ thị \((P)\) của hàm số khi \(m = 2\). 2. Dựa vào đồ thị \((P)\), biện luận theo k số nghiệm của phương trình:\({x^2} - 4x + k = 0\) 3. Tìm giá trị của \(m\) để hàm số nghịch biến trên khoảng \(\left( { - \infty ;2020} \right)\). Câu 2(2,5 điểm) Giải các phương … [Đọc thêm...] vềĐề thi mẫu HK1 Toán lớp 10 – số 9