Đề bài
Câu 1( 3,5 điểm) Cho hàm số :\(y = {x^2} – 2mx + 3\)
1. Khảo sát sự biến thiên và vẽ đồ thị \((P)\) của hàm số khi \(m = 2\).
2. Dựa vào đồ thị \((P)\), biện luận theo k số nghiệm của phương trình:\({x^2} – 4x + k = 0\)
3. Tìm giá trị của \(m\) để hàm số nghịch biến trên khoảng \(\left( { – \infty ;2020} \right)\).
Câu 2(2,5 điểm) Giải các phương trình sau:
1. \({x^2} – 2x – 5\left| {x – 1} \right| – 5 = 0\)
2. \(\sqrt {{x^2} – 3x + 3} – 2x + 3 = 0\)
Câu 3(1 điểm) Cho phương trình:
\({x^4} – 4{x^2} + a = 0\) (với \(a\) là tham số )
1. Giải phương trình đã cho khi \(a = – 5\)
2. Xác định \(a\) để phương trình đã cho có bốn nghiệm phân biệt thuộc đoạn \(\left[ { – 2;3} \right]\)
Câu 4(3 điểm)
Trong hệ trục tọa độ \((Oxy)\) cho bốn điểm:\(A\left( {2; – 1} \right),B\left( {3;4} \right),C\left( {4;3} \right),D\left( {3; – 2} \right)\)
1. Chứng minh bốn điểm đã cho tạo thành hình bình hành \(ABCD\). Tìm tọa độ tâm hình bình hành đó.
2. Gọi \(G\) là trọng tâm tam giác \(ABC\). Tìm tọa độ điểm \(E\) thỏa mãn: \(\overrightarrow {BE} = 2\overrightarrow {AD} – 3\overrightarrow {GC} \).
3. Lấy điểm \(M\) di động. Dựng điểm \(N\) sao cho \(\overrightarrow {MN} = \overrightarrow {MA} + 3\overrightarrow {MB} – 2\overrightarrow {MC} \). Chứng minh rằng \(MN\) luôn đi qua một điểm cố định.
Lời giải chi tiết
Câu 1(VD)
Phương pháp:
1.
Thay \(m = 2\) vào hàm số.
Tìm khoảng đồng biến, nghịch biến của hàm số.
Đồ thị: Xác định bề lõm, đỉnh và trục đối xứng của đồ thị và một số điểm thuộc đồ thị.
2.
Đặt hàm số của (P): \(y = f\left( x \right)\).
Đưa phương trình đã cho về dạng\(f\left( x \right) = g\left( x \right)\)
Số nghiệm của phương trình \(f\left( x \right) = g\left( x \right)\) là số giao điểm của hai đồ thị \(y = f\left( x \right)\) và \(y = g\left( x \right)\).
3. Tìm khoảng nghịch biến D của hàm số \(y = {x^2} – 2mx + 3\). Hàm số nghịch biến trên \(\left( { – \infty ;2020} \right)\) khi và chỉ khi \(\left( { – \infty ;2020} \right) \subset D\).
Giải:
1.
Thay \(m = 2\) vào hàm số ta được (P):\(y = {x^2} – 4x + 3\).
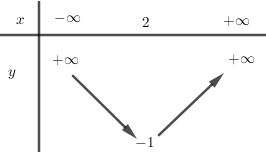
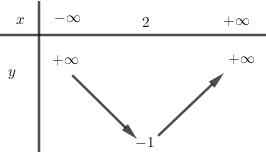
Do \(1 > 0\), hàm số đồng biến trên \(\left( {2; + \infty } \right)\), nghịch biến trên \(\left( { – \infty ;2} \right)\).
Bảng biến thiên:
Đồ thị:
Đồ thị có bề lõm hướng lên trên, đồ thị có đỉnh \(\left( {2; – 1} \right)\). Đồ thị nhận đường thẳng \(x = 2\) làm trục đối xứng.
Đồ thị đi qua điểm \(A\left( {0;3} \right),B\left( {1;0} \right),C\left( {3;0} \right)\).
2. Đặt \(f\left( x \right) = {x^2} – 4x + 3\)
\(\begin{array}{l}{x^2} – 4x + k = 0\left( 1 \right)\\ \Leftrightarrow {x^2} – 4x + 3 = 3 – k\end{array}\)
Số nghiệm của (1) bằng số giao điểm của \((P):y = f\left( x \right)\) và \(\left( d \right):y = 3 – k\).
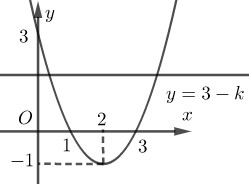
Từ đồ thị ta thấy:
Số giao điểm bằng 0 khi và chỉ khi \(3 – k < – 1 \Leftrightarrow k > 4\).
Số giao điểm bằng 1 khi và chỉ khi \(3 – k = – 1 \Leftrightarrow k = 4\).
Số giao điểm bằng 2 khi và chỉ khi \(3 – k > – 1 \Leftrightarrow k < 4\).
3.
Hàm số nghịch biến trên \(\left( { – \infty ;m} \right)\). Hàm số đã cho nghịch biến trên \(\left( { – \infty ;2020} \right)\) khi và chỉ khi \(\left( { – \infty ;2020} \right) \subset \left( { – \infty ;m} \right) \Leftrightarrow m \ge 2020\).
Câu 2(VD):
Phương pháp:
1. Đặt \(\left| {x – 1} \right| = t\left( {t \ge 0} \right)\), đưa phương trình về phương trình ẩn t.
2. \(\sqrt A = B \Leftrightarrow \left\{ \begin{array}{l}B \ge 0\\A = {B^2}\end{array} \right.\)
Giải:
1.
\({x^2} – 2x – 5\left| {x – 1} \right| – 5 = 0\)
\( \Leftrightarrow {\left( {x – 1} \right)^2} – 5\left| {x – 1} \right| – 6 = 0\)(1).
Đặt \(\left| {x – 1} \right| = t\left( {t \ge 0} \right)\). Phương trình (1) trở thành:
\({t^2} – 5t – 6 = 0 \Leftrightarrow t = 6\)
\(\begin{array}{l} \Leftrightarrow \left| {x – 1} \right| = 6 \Leftrightarrow \left[ \begin{array}{l}x – 1 = 6\\x – 1 = – 6\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = 7\\x = – 5\end{array} \right.\end{array}\)
2. \(\sqrt {{x^2} – 3x + 3} – 2x + 3 = 0\)
\(\begin{array}{l}\sqrt {{x^2} – 3x + 3} = 2x – 3\\ \Leftrightarrow \left\{ \begin{array}{l}x \ge \dfrac{3}{2}\\3{x^2} – 9x + 6 = 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x \ge \dfrac{3}{2}\\\left[ \begin{array}{l}x = 1\\x = 2\end{array} \right.\end{array} \right. \Leftrightarrow x = 2\end{array}\)
Câu 3(VD)
Phương pháp:
1. Thay \(a = – 5\) vào phương trình. Đặt \({x^2} = t\left( {t \ge 0} \right)\), đưa về phương trình ẩn t. Giải t tìm x.
2. Đưa về hai phương trình bậc hai
\(\begin{array}{l}{x^4} – 4{x^2} + a = 0\left( * \right)\\ \Leftrightarrow {\left( {{x^2} – 2} \right)^2} = 4 – a\\ \Leftrightarrow \left\{ \begin{array}{l}a < 4\\\left[ \begin{array}{l}{x^2} = 2 + \sqrt {4 – a} (1)\\{x^2} = 2 – \sqrt {4 – a} \left( 2 \right)\end{array} \right.\end{array} \right.\end{array}\)
(*) có 4 nghiệm phân biệt khi và chỉ khi (1) có 2 nghiệm phân biệt và (2) có 2 nghiệm phân biệt không trùng với phương trình (1).
Giải:
1. Thay \(a = – 5\) vào phương trình ta được \({x^4} – 4{x^2} – 5 = 0\)(1)
Đặt \({x^2} = t\left( {t \ge 0} \right)\), (1) trở thành:
\(\begin{array}{l}{t^2} – 4t – 5 = 0 \Leftrightarrow \left[ \begin{array}{l}t = – 1\\t = 5\end{array} \right.\\ \Leftrightarrow t = 5 \Leftrightarrow {x^2} = 5\end{array}\)
\(x = \pm \sqrt 5 \)
2.
\(\begin{array}{l}{x^4} – 4{x^2} + a = 0\left( * \right)\\ \Leftrightarrow {\left( {{x^2} – 2} \right)^2} = 4 – a\\ \Leftrightarrow \left\{ \begin{array}{l}a < 4\\\left[ \begin{array}{l}{x^2} = 2 + \sqrt {4 – a} (1)\\{x^2} = 2 – \sqrt {4 – a} \left( 2 \right)\end{array} \right.\end{array} \right.\end{array}\)
(*) có 4 nghiệm phân biệt khi và chỉ khi (1) có 2 nghiệm phân biệt và (2) có 2 nghiệm phân biệt không trùng với phương trình (1)
(2) có 2 nghiệm phân biệt \( \Leftrightarrow 2 – \sqrt {4 – a} > 0 \Leftrightarrow a > 0\)
Khi \(0 < a < 4\) các nghiệm của (*) đều thỏa mãn \({x^2} < 4\). Hay (*) luôn có có 4 nghiệm phân biệt thuộc đoạn \(\left[ { – 2;2} \right]\)
Vậy \(0 < a < 4\) thì phương trình đã cho có bốn nghiệm phân biệt thuộc đoạn \(\left[ { – 2;3} \right]\)
Câu 4(VD)
Phương pháp:
1. \(ABCD\) là hình bình hành \( \Leftrightarrow \overrightarrow {AB} = \overrightarrow {DC} \)
Tâm O của hình bình hành: \(\left\{ \begin{array}{l}{x_O} = \dfrac{{{x_A} + {x_C}}}{2}\\{y_O} = \dfrac{{{y_A} + {y_C}}}{2}\end{array} \right.\)
2. Tìm điểm G.
Sử dụng công thức: \(\overrightarrow {AD} = \overrightarrow {BD} – \overrightarrow {BA} \), tính chất trọng tâm \(\overrightarrow {BG} = \dfrac{2}{3}\overrightarrow {BO} \), tính chất trung điểm \(\overrightarrow {BO} = \dfrac{1}{2}\overrightarrow {BD} \).
3. Gọi \(I\) là trung điểm của \(MN\).
Sử dụng quy tắc cộng, trừ vectơ chứng minh \(I\) là điểm cố định.
Cách giải:
1.
Ta có \(\overrightarrow {AB} = \left( {3 – 2;4 – \left( { – 1} \right)} \right) = \left( {1;5} \right)\);\(\overrightarrow {DC} = \left( {4 – 3;3 – \left( { – 2} \right)} \right) = \left( {1;5} \right)\)
\( \Rightarrow \overrightarrow {AB} = \overrightarrow {DC} \)\( \Rightarrow ABCD\) là hình bình hành.
Tâm O của hình bình hành là chung điểm chung của AC và BD nên : \(\left\{ \begin{array}{l}{x_O} = \dfrac{{{x_A} + {x_C}}}{2} = 3\\{y_O} = \dfrac{{{y_A} + {y_C}}}{2} = 1\end{array} \right. \Rightarrow O\left( {3;1} \right)\)
2.
\(\begin{array}{l}\overrightarrow {BE} = 2\overrightarrow {AD} – 3\overrightarrow {GC} \\ = 2\left( {\overrightarrow {BD} – \overrightarrow {BA} } \right) – 3\left( {\overrightarrow {BC} – \overrightarrow {BG} } \right)\\ = 2\overrightarrow {BD} – 2\overrightarrow {BA} – 3\overrightarrow {BC} + 3\overrightarrow {BG} \\ = 2\overrightarrow {BD} – 2\overrightarrow {BD} – \overrightarrow {BC} + 3.\dfrac{2}{3}\overrightarrow {BO} \\\left. \begin{array}{l} = \overrightarrow {CB} + \overrightarrow {BD} = \overrightarrow {CD} \\\overrightarrow {CD} = \overrightarrow {BA} \end{array} \right\} \Rightarrow E \equiv A\end{array}\)
3.
\(\begin{array}{l}\overrightarrow {MN} = \overrightarrow {MA} + 3\overrightarrow {MB} – 2\overrightarrow {MC} \\ = \overrightarrow {MA} + \overrightarrow {MC} + 3\overrightarrow {CB} = 2\overrightarrow {MO} + 3\overrightarrow {CB} \\ \Leftrightarrow \overrightarrow {MN} – \overrightarrow {MO} – \overrightarrow {MO} = 3\overrightarrow {CB} \\ \Leftrightarrow \overrightarrow {ON} + \overrightarrow {OM} = 3\overrightarrow {CB} \\ \Leftrightarrow 2\overrightarrow {OI} = 3\overrightarrow {CB} \Leftrightarrow \overrightarrow {OI} = \dfrac{3}{2}\overrightarrow {CB} \end{array}\)
Do O,C,B là các điểm cố định nên I là điểm cố định.
Vậy MN luôn đi qua điểm cố định I.
