Câu hỏi: Mệnh đề nào dưới đây là sai? A. Góc giữa hai đường sinh đối xứng qua trục của mặt nón bằng góc ở đỉnh của mặt nón. B. Diện tích xung quanh của hình nón tròn xoay là giới hạn của diện tích xung quanh của hình chóp đều ngoại tiếp hình nón đó, khi số cạnh đáy tăng lên vô hạn C. Diện tích xung quanh của hình nón bằng một nửa tích của chu vi đáy với độ dài đường … [Đọc thêm...] vềMệnh đề nào dưới đây là sai?
Kết quả tìm kiếm cho: ty+so
Cho khối nón có độ dài đường sinh bằng (2a ) và bán kính đáy bằng (a ). Thể tích của khối nón đã cho bằng
Câu hỏi: Cho khối nón có độ dài đường sinh bằng (2a ) và bán kính đáy bằng (a ). Thể tích của khối nón đã cho bằng A. \( \frac{{\sqrt 3 \pi {a^3}}}{3}\) B. \( \frac{{\sqrt 3 \pi {a^3}}}{2}\) C. \( \frac{{\sqrt 3 \pi {a^3}}}{4}\) D. \( \frac{{\sqrt 3 \pi {a^3}}}{5}\) Lời Giải: Đây là các bài toán về Mặt nón, Hình nón, Khối nón trong Phần Mặt tròn xoay. ét … [Đọc thêm...] vềCho khối nón có độ dài đường sinh bằng (2a ) và bán kính đáy bằng (a ). Thể tích của khối nón đã cho bằng
Cho mặt cầu tâm (O ) bán kính (R ). Xét mặt phẳng (P) thay đổi cắt mặt cầu theo giao tuyến là đường tròn (C). Hình nón (N ) có đỉnh (S ) nằm trên mặt cầu, có đáy là đường tròn (C) và có chiều cao h (h > R ). Tìm (h ) để thể tích khối nón được tạo nên bởi (N) có giá trị lớn nhất.
Câu hỏi: Cho mặt cầu tâm (O ) bán kính (R ). Xét mặt phẳng (P) thay đổi cắt mặt cầu theo giao tuyến là đường tròn (C). Hình nón (N ) có đỉnh (S ) nằm trên mặt cầu, có đáy là đường tròn (C) và có chiều cao h (h > R ). Tìm (h ) để thể tích khối nón được tạo nên bởi (N) có giá trị lớn nhất. A. \(h = R\sqrt 3 \) B. \(h = R\sqrt 2 \) C. \( h = … [Đọc thêm...] vềCho mặt cầu tâm (O ) bán kính (R ). Xét mặt phẳng (P) thay đổi cắt mặt cầu theo giao tuyến là đường tròn (C). Hình nón (N ) có đỉnh (S ) nằm trên mặt cầu, có đáy là đường tròn (C) và có chiều cao h (h > R ). Tìm (h ) để thể tích khối nón được tạo nên bởi (N) có giá trị lớn nhất.
Cho hình nón có góc ở đỉnh bằng 1200 và đường cao bằng (2. ) Tính diện tích xung quanh của hình nón đã cho.
Câu hỏi: Cho hình nón có góc ở đỉnh bằng 1200 và đường cao bằng (2. ) Tính diện tích xung quanh của hình nón đã cho. A. \(16\sqrt 3 \pi \) B. \(8\sqrt 3 \pi \) C. \(4\sqrt 3 \pi \) D. \(8\pi \) Lời Giải: Đây là các bài toán về Mặt nón, Hình nón, Khối nón trong Phần Mặt tròn xoay. Gọi S là đỉnh hình nón, AB là 1 đường kính của hình nón và O là tâm đường tròn … [Đọc thêm...] vềCho hình nón có góc ở đỉnh bằng 1200 và đường cao bằng (2. ) Tính diện tích xung quanh của hình nón đã cho.
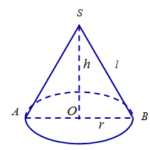
Cho hình nón tròn xoay có bán kính đường tròn đáy r, chiều cao h và đường sinh \(l\). Kết luận nào sau đây sai?
Câu hỏi: Cho hình nón tròn xoay có bán kính đường tròn đáy r, chiều cao h và đường sinh \(l\). Kết luận nào sau đây sai? A. \(V = \frac{1}{3}\pi {r^2}h\) B. \({S_{tp}} = \pi rl + \pi {r^2}\) C. \({h^2} = {r^2} + {l^2}\) D. \({S_{xq}} = \pi rl\) Lời Giải: Đây là các bài toán về Mặt nón, Hình nón, Khối nón trong Phần Mặt tròn xoay. Ta có tam giác SOB vuông tại O … [Đọc thêm...] vềCho hình nón tròn xoay có bán kính đường tròn đáy r, chiều cao h và đường sinh \(l\). Kết luận nào sau đây sai?
Cho hình nón tròn xoay có đỉnh là S, O là tâm của đường tròn đáy, đường sinh bằng \(a\sqrt2\) và góc giữa đường sinh và mặt phẳng đáy bằng 600. Diện tích xung quanh Sxq của hình nón và thể tích V của khối nón tương ứng là:
Câu hỏi: Cho hình nón tròn xoay có đỉnh là S, O là tâm của đường tròn đáy, đường sinh bằng \(a\sqrt2\) và góc giữa đường sinh và mặt phẳng đáy bằng 600. Diện tích xung quanh Sxq của hình nón và thể tích V của khối nón tương ứng là: A. \( {S_{xq}} = \pi {a^2},V = \frac{{\pi {a^3}\sqrt 6 }}{4}\) B. \( {S_{xq}} = \frac{{\pi {a^2}}}{2},V = \frac{{\pi {a^3}\sqrt 3 … [Đọc thêm...] vềCho hình nón tròn xoay có đỉnh là S, O là tâm của đường tròn đáy, đường sinh bằng \(a\sqrt2\) và góc giữa đường sinh và mặt phẳng đáy bằng 600. Diện tích xung quanh Sxq của hình nón và thể tích V của khối nón tương ứng là:
Lấy ngẫu nhiên hai viên bi từ một thùng gồm 4 bi xanh, 5 bi đỏ và 6 bi vàng. Tính xác suất để lấy được hai viên bi khác màu?
Câu hỏi: Lấy ngẫu nhiên hai viên bi từ một thùng gồm 4 bi xanh, 5 bi đỏ và 6 bi vàng. Tính xác suất để lấy được hai viên bi khác màu? A. 67,6% B. 29,5% C. 32,4% D. 70,5% Lời Giải: Đây là các bài toán về Hoán vị, Chỉnh hợp, Tổ hợp có áp dụng các phép đếm. • Số phần tử của không gian mẫu \(n\left( \Omega \right) = C_{15}^2\) • Gọi A là biến cố "lấy được hai bi … [Đọc thêm...] vềLấy ngẫu nhiên hai viên bi từ một thùng gồm 4 bi xanh, 5 bi đỏ và 6 bi vàng. Tính xác suất để lấy được hai viên bi khác màu?
Trên giá sách có 4 quyển sách toán, 3 quyển sách lý, 2 quyển sách hóa. Lấy ngẫu nhiên 3 quyển sách. Tính xác suất để được 3 quyển được lấy ra có ít nhất một quyển là toán.
Câu hỏi: Trên giá sách có 4 quyển sách toán, 3 quyển sách lý, 2 quyển sách hóa. Lấy ngẫu nhiên 3 quyển sách. Tính xác suất để được 3 quyển được lấy ra có ít nhất một quyển là toán. A. \(\frac{2}{7}\) B. \(\frac{3}{4}\) C. \(\frac{{37}}{{42}}\) D. \(\frac{{10}}{{21}}\) Lời Giải: Đây là các bài toán về Hoán vị, Chỉnh hợp, Tổ hợp có áp dụng các phép đếm. Tổng số … [Đọc thêm...] vềTrên giá sách có 4 quyển sách toán, 3 quyển sách lý, 2 quyển sách hóa. Lấy ngẫu nhiên 3 quyển sách. Tính xác suất để được 3 quyển được lấy ra có ít nhất một quyển là toán.
Gieo ngẫu nhiên hai con xúc sắc cân đối và đồng chất. Xác suất của biến cố “ Có ít nhất một con xúc sắc xuất hiện mặt một chấm” là:
Câu hỏi: Gieo ngẫu nhiên hai con xúc sắc cân đối và đồng chất. Xác suất của biến cố “ Có ít nhất một con xúc sắc xuất hiện mặt một chấm” là: A. \(\frac{11}{36}\) B. \(\frac{1}{6}\) C. \(\frac{25}{36}\) D. \(\frac{15}{36}\) Lời Giải: Đây là các bài toán về Hoán vị, Chỉnh hợp, Tổ hợp có áp dụng các phép đếm. Gọi A … [Đọc thêm...] vềGieo ngẫu nhiên hai con xúc sắc cân đối và đồng chất. Xác suất của biến cố “ Có ít nhất một con xúc sắc xuất hiện mặt một chấm” là:
Một tổ gồm 9 em, trong đó có 3 nữ được chia thành 3 nhóm đều nhau. Tính xác xuất để mỗi nhóm có một nữ.
Câu hỏi: Một tổ gồm 9 em, trong đó có 3 nữ được chia thành 3 nhóm đều nhau. Tính xác xuất để mỗi nhóm có một nữ. A. \(\frac{3}{56}\) B. \(\frac{27}{84}\) C. \(\frac{53}{56}\) D. \(\frac{19}{28}\) Lời Giải: Đây là các bài toán về Hoán vị, Chỉnh hợp, Tổ hợp có áp dụng các phép đếm. +Số phần tử trong không gian mẫu: Chọn ngẫu nhiên 3 em trong 9 … [Đọc thêm...] vềMột tổ gồm 9 em, trong đó có 3 nữ được chia thành 3 nhóm đều nhau. Tính xác xuất để mỗi nhóm có một nữ.