Trả lời câu hỏi trong bài 2 Tổng và hiệu của hai vectơ - Chân trời ============ KHỞI ĐỘNGMột kiện hàng được vận chuyển từ điểm A đến điểm B rồi lại được vận chuyển từ điểm B đến điểm C. Tìm vectơ biểu diễn tổng của hai độ dịch chuyển: $\vec{AB}$ + $\vec{BC}$ Hướng dẫn giải: Vectơ biểu diễn tổng của hai độ dịch chuyển: $\vec{AB}$ + $\vec{BC}$ là vectơ $\vec{AC}$1. … [Đọc thêm...] vềTrả lời câu hỏi trong bài 2 Tổng và hiệu của hai vectơ – Chân trời
Kết quả tìm kiếm cho: hình bình hành có 1 góc vuông
Lý thuyết Bài 11: Tích vô hướng của hai vectơ – Kết nối
Lý thuyết Bài 11: Tích vô hướng của hai vectơ ============= Tóm tắt lý thuyết 1.1. Góc giữa hai vectơ Cho hai vectơ \(\overrightarrow u \) và \(\overrightarrow v \) khác \({\vec 0}\). Từ một điểm A tuỳ ý, vẽ các vectơ \(\overrightarrow {AB} = \overrightarrow u \) và \(\overrightarrow {AC} = \overrightarrow v \) (Hình cho bên dưới). Khi đó, … [Đọc thêm...] vềLý thuyết Bài 11: Tích vô hướng của hai vectơ – Kết nối
Lý thuyết Bài 8: Tổng và hiệu của hai vectơ – Kết nối
Lý thuyết Bài 8: Tổng và hiệu của hai vectơ ============= Tóm tắt lý thuyết 1.1. Tổng của hai vectơ Cho hai vectơ \(\overrightarrow a ,\overrightarrow b \). Lấy một điểm A tuỳ ý và vẽ \(\overrightarrow {AB} = \overrightarrow a ,\overrightarrow {BC} = \overrightarrow b \) (Hình bên dưới). Khi đó vectơ \(\overrightarrow {AC} \) được gọi … [Đọc thêm...] vềLý thuyết Bài 8: Tổng và hiệu của hai vectơ – Kết nối
Trả lời câu hỏi trong bài 1 Mệnh đề – Chân trời
Trả lời câu hỏi trong bài 1 Mệnh đề - Chân trời ============ KHỞI ĐỘNGHãy theo dõi tình huống sau đây:Bạn có thể phát biểu định lí theo cách khác? Hướng dẫn giải: Tam giác ABC cân khi và chỉ khi tam giác ABC có hai góc ở đáy bằng nhau.Để tam giác ABC cân, điều kiện cần và đủ là hai góc ở đáy bằng nhau...1. MỆNH ĐỀ Khám phá 1: Xét các câu sau đây:1 + 1 = 2Dân ca … [Đọc thêm...] vềTrả lời câu hỏi trong bài 1 Mệnh đề – Chân trời
Bài 43: Ôn tập hình học và đo lường – SGK Kết nối tri thức
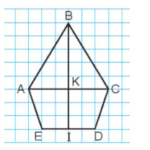
Giải bài tập thực hành Bài 43: Ôn tập hình học và đo lường - SGK Kết nối tri thức ============ Chuyên mục: Giải bài tập Toán 3 - SGK Kết nối tri thức ============= Luyện tập 1 Bài tập1. Sgk Toán 3 tập 1 Trong hình bên:a) Có mấy góc vuông?b) Có mấy góc không vuông đỉnh A?c) Tìm trung điểm của đoạn thẳng AC và đoạn thẳng ED Lời giải: a) Có 6 góc vuông là các góc: AKB; … [Đọc thêm...] vềBài 43: Ôn tập hình học và đo lường – SGK Kết nối tri thức
Bài: Góc vuông. Góc không vuông – SGK Cánh Diều
Giải bài tập thực hành Bài: Góc vuông. Góc không vuông ============ Chuyên mục: Giải bài tập Toán 3 - Cánh diều ============= 12/06/2022 by Minh Đạo Để lại bình luận Giải bài: Góc vuông. Góc không vuông sách cánh diều toán 3 tập 1. Phần đáp án chuẩn, hướng dẫn giải chi tiết cho từng câu hỏi có trong chương trình học của sách giáo khoa. Hi vọng, các em học sinh hiểu … [Đọc thêm...] vềBài: Góc vuông. Góc không vuông – SGK Cánh Diều
(Sở Thái Nguyên 2022) Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác vuông tại \(B\), \(AB = 6\sqrt 3 ,\widehat {CAB} = 30^\circ \). Đỉnh \(S\) cách đều ba điểm \(A,B,C\) và cạnh bên \(SB\) tạo với mặt phẳng \(\left( {ABC} \right)\) một góc \(45^\circ \). Hai điểm \(M,Q\) lần lượt thuộc các đoạn \(AB\) và \(SB\) sao cho \(AM = 2MB,QB = 2QS\). Mặt phẳng \(\left( \alpha \right)\) chứa \(M,Q\) và song song với đường thẳng \(BC\) chia khối chóp \(S.ABC\) thành hai khối đa diện có thể tích lần lượt là \({V_1},{V_2}\left( {{V_1} < {V_2}} \right)\). Giá trị của \({V_2}\) là
Câu hỏi:
(Sở Thái Nguyên 2022) Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác vuông tại \(B\), \(AB = 6\sqrt 3 ,\widehat {CAB} = 30^\circ \). Đỉnh \(S\) cách đều ba điểm \(A,B,C\) và cạnh bên \(SB\) tạo với mặt phẳng \(\left( {ABC} \right)\) một góc \(45^\circ \). Hai điểm \(M,Q\) lần lượt thuộc các đoạn \(AB\) và \(SB\) sao cho \(AM = 2MB,QB = 2QS\). Mặt phẳng … [Đọc thêm...] về (Sở Thái Nguyên 2022) Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác vuông tại \(B\), \(AB = 6\sqrt 3 ,\widehat {CAB} = 30^\circ \). Đỉnh \(S\) cách đều ba điểm \(A,B,C\) và cạnh bên \(SB\) tạo với mặt phẳng \(\left( {ABC} \right)\) một góc \(45^\circ \). Hai điểm \(M,Q\) lần lượt thuộc các đoạn \(AB\) và \(SB\) sao cho \(AM = 2MB,QB = 2QS\). Mặt phẳng \(\left( \alpha \right)\) chứa \(M,Q\) và song song với đường thẳng \(BC\) chia khối chóp \(S.ABC\) thành hai khối đa diện có thể tích lần lượt là \({V_1},{V_2}\left( {{V_1} < {V_2}} \right)\). Giá trị của \({V_2}\) là
(THPT Lê Thánh Tông – HCM-2022) Cho lăng trụ \(ABC.A’B’C’\) có tam giác \(ABC\) vuông cân tại \(A\). Hình chiếu vuông góc của \(A’\) lên mặt đáy trùng với trung điểm của cạnh \(BC\). Biết cạnh \(AA’ = a\sqrt 3 \) và tạo với mặt đáy của hình lăng trụ một góc bằng \(60^\circ \). Khoảng cách từ đỉnh \(C’\) đến mặt \(\left( {A’BC} \right)\) bằng
Câu hỏi:
(THPT Lê Thánh Tông - HCM-2022) Cho lăng trụ \(ABC.A'B'C'\) có tam giác \(ABC\) vuông cân tại \(A\). Hình chiếu vuông góc của \(A'\) lên mặt đáy trùng với trung điểm của cạnh \(BC\). Biết cạnh \(AA' = a\sqrt 3 \) và tạo với mặt đáy của hình lăng trụ một góc bằng \(60^\circ \). Khoảng cách từ đỉnh \(C'\) đến mặt \(\left( {A'BC} \right)\) bằng
A. … [Đọc thêm...] về (THPT Lê Thánh Tông – HCM-2022) Cho lăng trụ \(ABC.A’B’C’\) có tam giác \(ABC\) vuông cân tại \(A\). Hình chiếu vuông góc của \(A’\) lên mặt đáy trùng với trung điểm của cạnh \(BC\). Biết cạnh \(AA’ = a\sqrt 3 \) và tạo với mặt đáy của hình lăng trụ một góc bằng \(60^\circ \). Khoảng cách từ đỉnh \(C’\) đến mặt \(\left( {A’BC} \right)\) bằng
Giải bài Ôn tập hình học và đo lường | Giải toán 3 tập 2 chân trời sáng tạo
Giải bài tập thực hành Giải bài Ôn tập hình học và đo lường | Giải toán 3 tập 2 chân trời sáng tạo ============ Chuyên mục: Giải bài tập Toán 3 - Chân trời ============= LUYỆN TẬP Bài tập 1. Trang 82 sgk toán 3 tập 2 Số?a) 1 m = .?. dm 1 km = .?. m = .?. cm 1 dm = .?. cm = .?. … [Đọc thêm...] vềGiải bài Ôn tập hình học và đo lường | Giải toán 3 tập 2 chân trời sáng tạo
Bài 5: Khoảng cách – Hình học 11
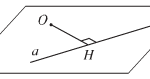
1. Tóm tắt lý thuyết 1.1. Khoảng cách từ một điểm đến một đường thẳng, đến một mặt phẳng a) Khoảng cách từ một điểm đến một đường thẳng Cho điểm O và đường thẳng a. Trong mặt phẳng (O, a) gọi H là hình chiếu vuông góc của O trên a. Khi đó khoảng cách giữa O và H được gọi là khoảng cách từ điểm O đến đường thẳng a. Kí hiệu d(O, a). … [Đọc thêm...] vềBài 5: Khoảng cách – Hình học 11