Lý thuyết Bài 8: Tổng và hiệu của hai vectơ – Kết nối

Lý thuyết Bài 8: Tổng và hiệu của hai vectơ
=============

Tóm tắt lý thuyết

1.1. Tổng của hai vectơ

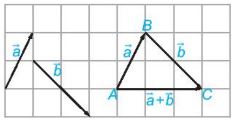
– Quy tắc ba điểm: Với ba điểm bắt kì A, B, C, ta có \(\overrightarrow {AB}  + \overrightarrow {BC}  = \overrightarrow {AC} \)

– Quy tắc hình bình hành: Nếu ABCD là một hình binh hành thì \(\overrightarrow {AB}  + \overrightarrow {AD}  = \overrightarrow {AC} \) 

– Với ba vectơ \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \) tuỳ ý:

• Tính chất giao hoán: \(\overrightarrow a  + \overrightarrow b  = \overrightarrow b  + \overrightarrow a \)
• Tính chất kết hợp: \(\left( {\overrightarrow a  + \overrightarrow b } \right) + \overrightarrow c  = \overrightarrow a  + \left( {\overrightarrow b  + \overrightarrow c } \right)\)
• Tính chất của vectơ-không: \(\overrightarrow a  + \overrightarrow 0  = \overrightarrow 0  + \overrightarrow a  = \overrightarrow a \) 

Chú ý:  Do các vectơ \(\left( {\overrightarrow a  + \overrightarrow b } \right) + \overrightarrow c \) và \(\overrightarrow a  + \left( {\overrightarrow b  + \overrightarrow c } \right)\) bằng nhau, nên ta còn viết chúng dưới dạng \(\overrightarrow a  + \overrightarrow b  + \overrightarrow c \) và gọi là tổng cửa ba vectơ \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \). Tương tự, ta cũng có thể viết tổng của một số vectơ mà không cần dùng các dấu ngoặc. 

Ví dụ:  Cho hình Vuông ABCD với cạnh có độ dài bằng 1. Tính độ dài của các vectơ \(\overrightarrow {AB}  + \overrightarrow {CB} ,\overrightarrow {AB}  + \overrightarrow {DC}  + \overrightarrow {BD} \). 

Giải

Do \(\overrightarrow {AB}  = \overrightarrow {DC} \) nên \(\overrightarrow {AB}  + \overrightarrow {CB}  = \overrightarrow {DC}  + \overrightarrow {CB}  = \overrightarrow {DB} \)

Vậy \(\left| {\overrightarrow {AB}  + \overrightarrow {CB} } \right| = \left| {\overrightarrow {DB} } \right| = DB = \sqrt 2 \)

Ta có \(\overrightarrow {AB}  + \overrightarrow {DC}  + \overrightarrow {BD}  = \left( {\overrightarrow {AB}  + \overrightarrow {BD} } \right) + \overrightarrow {DC}  = \overrightarrow {AD}  + \overrightarrow {DC}  = \overrightarrow {AC} \) 

Do đó \(\left| {\overrightarrow {AB}  + \overrightarrow {DC}  + \overrightarrow {BD} } \right| = AC = \sqrt 2 \) 

1.2. Hiệu của hai vectơ

Chú ý: Hai vectơ đối nhau khi và chỉ khi tổng của chúng bằng \(\overrightarrow 0 \).

Chú ý: Nếu \(\overrightarrow b  + \overrightarrow c  = \overrightarrow a \) thì \(\overrightarrow a  – \overrightarrow b  = \overrightarrow a  + \left( { – \overrightarrow b } \right) = \overrightarrow c  + \overrightarrow b  + \left( { – \overrightarrow b } \right) = \overrightarrow c  + \overrightarrow 0  = \overrightarrow c \)

Với ba điểm O, M, N tuỷ ý, ta có \(\overrightarrow {MN}  = \overrightarrow {MO}  + \overrightarrow {ON}  = \left( { – \overrightarrow {OM} } \right) + \overrightarrow {ON}  = \overrightarrow {ON}  – \overrightarrow {OM} \)

– Quy tắc hiệu: Với ba điểm O, M, N, ta có \(\overrightarrow {MN}  = \overrightarrow {ON}  – \overrightarrow {OM} \)

Ví dụ: Cho hình bình hành ABCD và một điểm O bất kì.

Chứng minh rằng \(\overrightarrow {OB}  – \overrightarrow {OA}  = \overrightarrow {OC}  – \overrightarrow {OD} \) 

Giải

Áp dụng quy tắc hiệu, ta có \(\overrightarrow {OB}  – \overrightarrow {OA}  = \overrightarrow {AB} ,\overrightarrow {OC}  – \overrightarrow {OD}  = \overrightarrow {DC} \)

Mặt khác \(\overrightarrow {AB}  = \overrightarrow {DC} \) nên \(\overrightarrow {OB}  – \overrightarrow {OA}  = \overrightarrow {OC}  – \overrightarrow {OD} \)

Chú ý:  Phép cộng vectơ tương ứng với các quy tắc tổng hợp lực, tổng hợp vận tốc:

+ Nếu hai lực cùng tác động vào chất điểm A và được biểu diễn bởi các vectơ \(\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} \) thì hợp lực tác động vào A được biểu diễn bởi vectơ \(\overrightarrow {{u_1}}  + \overrightarrow {{u_2}} \)

+ Nếu một con thuyền dĩ chuyển trên sông với vận tốc riêng (vận tốc so với dòng nước) được biểu diễn bởi vectơ \(\overrightarrow {{v_r}} \) và vận tốc của dòng nước (so với bờ) được biểu diễn bởi vectơ \(\overrightarrow {{v_n}} \) thì vận tốc thực tế của thuyền (so với bờ) được biểu diễn bởi vectơ \(\overrightarrow {{v_r}}  + \overrightarrow {{v_n}} \). 

Bài tập minh họa

Câu 1: 

Một con tàu chuyển động từ bờ bên này sang bờ bên kia của một dòng sông với vận tốc riêng không đổi. Giả sử vận tốc dòng nước là không đổi và đáng kể, các yếu tố bên ngoài khác không ảnh hưởng đến vận tốc thực tế của tàu. Nếu không quan tâm đến điểm đến thì cần giữ lái cho tàu tạo với bờ sông một góc bao nhiêu để tàu sang bờ bên kia được nhanh nhất?

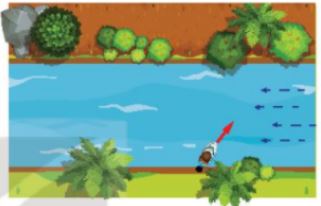
Hướng dẫn giải

Gọi: vận tốc thực tế của tàu là \(\overrightarrow v \)

Vận tốc riêng của tàu (đối với dòng nước) là \(\overrightarrow {{v_t}} \)

Vận tốc của dòng nước (đối với bờ) là \(\overrightarrow {{v_n}} \)

Ta có: \(\overrightarrow v  = \overrightarrow {{v_n}}  + \overrightarrow {{v_t}} \)

Để tàu sang bờ bên kia nhanh nhất thì vận tốc thực tế của tàu có hướng vuông góc với bờ.

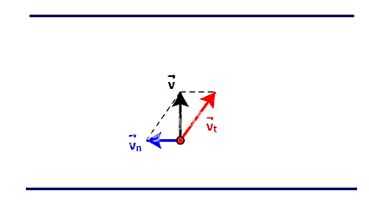
Thao quy tắc hình bình hành thì \(\overrightarrow v \) là vecto đường chéo xuất phát từ gốc chung của vecto vận tốc riêng của tàu và vecto vận tốc dòng nước tác động lên tàu.

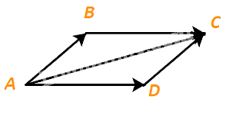
Câu 2: Cho hình bình hành ABCD. Tìm mối quan hệ giữa hai vectơ \(\overrightarrow {AB}  + \overrightarrow {AD} \) và \(\overrightarrow {AC} \)

Hướng dẫn giải

Vì ABCD là hình bình hành nên \(\left\{ \begin{array}{l}AD//\;BC\\AD = BC\end{array} \right.\), hay \(\overrightarrow {AD}  = \overrightarrow {BC} \).

Do đó \(\overrightarrow {AB}  + \overrightarrow {AD}  = \overrightarrow {AB}  + \overrightarrow {BC}  = \overrightarrow {AC} \).

=============
– Học Toán lớp 10 – Kết nối