Trả lời câu hỏi trong bài 10 Vectơ trong mặt phẳng tọa độ – Kết nối

Trả lời câu hỏi trong bài 10 Vectơ trong mặt phẳng tọa độ
=============

1. TỌA ĐỘ CỦA VECTƠ

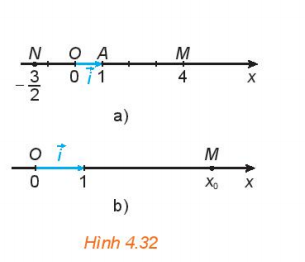
Hoạt động 1:  Trên trục số Ox, gọi A là điểm biểu diến số 1 và đặt $\overrightarrow{OA}=\overrightarrow{i}$ (H4.32a). Gọi M là điểm biểu diễn số 4, N là điểm biểu diễn số $\frac{-3}{2}$. Hãy biểu thị mỗi vecto $\overrightarrow{OM}=\overrightarrow{ON}$ theo vecto $\overrightarrow{i}$. 

Hướng dẫn giải:

• $\overrightarrow{OM}=4\overrightarrow{i}$
• $\overrightarrow{ON}=\frac{-3}{2}\overrightarrow{i}$

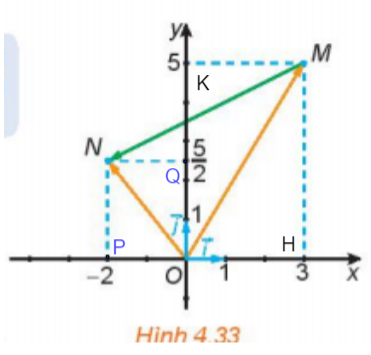
Hoạt động 2:  Trong Hình 4.33:

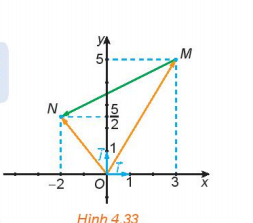
a. Hãy biểu thị mỗi vecto $\overrightarrow{OM},\overrightarrow{ON}$ theo các vecto $\overrightarrow{i};\overrightarrow{j}$.

b. Hãy biểu thị vecto $\overrightarrow{MN}$ theo các vecto $\overrightarrow{OM},\overrightarrow{ON}$, từ đó biểu thị vecto $\overrightarrow{MN}$ theo các vecto $\overrightarrow{i};\overrightarrow{j}$.

Hướng dẫn giải:

a. Ta có:

• $\overrightarrow{OM} = \overrightarrow{OH}+ \overrightarrow{OK} $

= $3\overrightarrow{i} + 5\overrightarrow{j}$.

• $\overrightarrow{ON} = \overrightarrow{OP}+ \overrightarrow{OQ} $

= $-2\overrightarrow{i} + \frac{5}{2}\overrightarrow{j}$.

b. $\overrightarrow{MN} = \overrightarrow{ON}+ \overrightarrow{OM} $

= $-2\overrightarrow{i} + \frac{5}{2}\overrightarrow{j}$ – ($3\overrightarrow{i} + 5\overrightarrow{j}$)

= $-5\overrightarrow{i} + \frac{-5}{2}\overrightarrow{j}$

Luyện tập 1:  Tìm tọa độ của $\overrightarrow{0} $

Hướng dẫn giải:

$\overrightarrow{0} $ có tọa độ là (0; 0).

2. BIỂU THỨC TỌA ĐỘ CỦA CÁC PHÉP TOÁN VECTƠ

Hoạt động 3:  Trong mặt phẳng tọa độ Oxy, cho $\overrightarrow{u}$= (2; -3), $\overrightarrow{v} $ = (4;1), $\overrightarrow{a} $ = (8;-12).

a. Hãy biểu thị mỗi vecto $\overrightarrow{u}$, $\overrightarrow{v}$, $\overrightarrow{a}$ theo các vecto $\overrightarrow{i}$, $\overrightarrow{j}$.

b. Tìm tọa độ của các vecto $\overrightarrow{u} + \overrightarrow{v}$, $\overrightarrow{4u}$.

c. Tìm mối liên hệ giữa hai vecto $\overrightarrow{u}$, $\overrightarrow{a}$.

Hướng dẫn giải:

a.

• $\overrightarrow{u}$ = $2\overrightarrow{i} + (-3)\overrightarrow{j}$
• $\overrightarrow{v}$ = $4\overrightarrow{i} + 1\overrightarrow{j}$.
• $\overrightarrow{a}$ = $8\overrightarrow{i} + (-12)\overrightarrow{j}$

b.

• $\overrightarrow{u} + \overrightarrow{v}$ = $6\overrightarrow{i} + (-2)\overrightarrow{j}$ nên có tọa độ là (6; -2).
• $\overrightarrow{4u}$ = $8\overrightarrow{i} + (-12)\overrightarrow{j}$ nên có tọa độ là (8; -12)

c. $\overrightarrow{4u}$=$\overrightarrow{a}$.

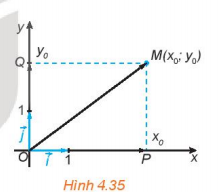
Hoạt động 4:  Trong mặt phẳng tọa độ Oxy, cho điểm M(x_o; y_o). Gọi P, Q tương ứng là hình chiếu vuông góc của M trên trục hoành Ox và trục tung Oy.

a. Trên trục Ox, điểm P biểu diễn số nào? Biểu thị $\overrightarrow{OP}$ theo $\overrightarrow{i}$ và tính độ dài của $\overrightarrow{OP}$ theo x_o.

b. Trên trục Oy, điểm Q biểu diễn số nào? Biểu thị $\overrightarrow{OQ}$ theo $\overrightarrow{j}$ và tính độ dài của $\overrightarrow{OQ}$ theo y_o.

c. Dựa vào hình chữ nhật OPMQ, tính độ dài của $\overrightarrow{OM}$ theo x_o; y_o.

d. Biểu thị $\overrightarrow{OM}$ theo các vecto $\overrightarrow{i};\overrightarrow{j}$.

Hướng dẫn giải:

a. Điểm P biểu diễn số x_o.

$\overrightarrow{OP}$ = $x_{o}\overrightarrow{i} $

$|\overrightarrow{OP}|$ = |x_o |

b. Điểm Q biểu diễn số y_o.

$\overrightarrow{OQ}$ = $y_{o}\overrightarrow{j} $

$|\overrightarrow{OQ}|$ = |y_o |

c. $|\overrightarrow{OM}|$ = $\sqrt{OP^{2}+MP^{2}}$= $\sqrt{OP^{2}+MP^{2}}$=$\sqrt{x_{o}^{2}+y_{o}^{2}}$

d. $\overrightarrow{OM}$ = $x_{o}\overrightarrow{i} + y_{o}\overrightarrow{j}$.

Hoạt động 5:  Trong mặt phẳng tọa độ Oxy, cho các điểm M(x; y) và N(x’; y’).

a. Tìm tọa độ của các vecto $\overrightarrow{OM}, \overrightarrow{ON}$

b. Biểu thị vecto $\overrightarrow{MN}$ theo các vecto$\overrightarrow{OM}, \overrightarrow{ON}$ và tìm tọa độ của $\overrightarrow{MN}$ .

c. Tìm độ dài của vecto $\overrightarrow{MN}$.

Hướng dẫn giải:

a. $\overrightarrow{OM}(x;y)$; $\overrightarrow{ON}(x’;y’)$

b. $\overrightarrow{MN}$= $\overrightarrow{ON} – \overrightarrow{OM}$

=> $\overrightarrow{MN}(x’-x;y’-y)$

c. $|\overrightarrow{MN}|$ = $\sqrt{(x’-x)^{2}+(y’-y)^{2}}$.

Luyện tập 2:  Trong mặt phẳng tọa độ Oxy, cho hai điểm A(2; 1). B(3; 3).

a. Các điểm O, A, B có thẳng hàng hay không?

b. Tìm điểm M(x; y) để OABM là một hình bình hành.

Hướng dẫn giải:

a. Xét vecto: $\overrightarrow{OA}(2;1)$ và $\overrightarrow{OB}(3;3)$ không cùng phương vì $\frac{2}{3}\neq \frac{1}{3}$. Do đó các điểm O, A, B không thẳng hàng.

b. OABM là hình bình hành khi  và chỉ khi $\overrightarrow{OA}$ = $\overrightarrow{MB}$.

Ta có: $\overrightarrow{OA}(2;1)$ và $\overrightarrow{MB}(3-x;3-y)$

$\overrightarrow{OA}$ = $\overrightarrow{MB}$ $\Leftrightarrow \left\{\begin{matrix}3-x=2\\ 3-y=1\end{matrix}\right.$

$\Leftrightarrow x=1; y=2$

Vậy điểm cần tìm là M(1; 2).

Vận dụng:  Từ thông tin dự báo bão được đưa ra ở đầu bài học, hãy xác định tọa độ vị trí M của tâm bão tại thời điểm 9 giờ trong khoảng thời gian 12 giờ của dự báo.

Hướng dẫn giải:

Gọi điểm A(13,8; 108,3), B(14,2; 106,3) và điểm M(x; y).

Vì trong 12 giờ tâm bão đi từ A đến B và M là vị trí của tâm bão lúc 9 giờ nên ta có mỗi quan hệ của AM và AB là: AM = $\frac{9}{12}=\frac{3}{4}$AB

=> $\overrightarrow{AM}=\frac{3}{4}\overrightarrow{AB}$

Ta có: $\overrightarrow{AM}(x-13,8; y-108,3)$ và $\overrightarrow{AB}(0,3; -2$

$\overrightarrow{AM}=\frac{3}{4}\overrightarrow{AB}$

$\Leftrightarrow \left\{\begin{matrix}x-13,8=\frac{3}{4}.0,3\\ y-108,3=\frac{3}{4}.(-2)\end{matrix}\right.$

$\Leftrightarrow x = 14,025; y= 106,8$.

Vậy M(14,025; 106,8)

=============
– Học Toán lớp 10 – Kết nối