Sách Toán - Học toán

Giải bài tập Toán từ lớp 1 đến lớp 12, Học toán online và Đề thi toán

Kết quả tìm kiếm cho: Lau Ong Hoang

Giải bài 2 Đa thức một biến, nghiệm của đa thức một biến – Chương 6 Toán 7 Cánh diều

Ngày Thuộc chủ đề:Giải bài tập Toán 7 – Cánh diều Tag với:

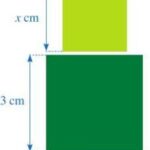
Giải bài 1 Biểu thức số. Biểu thức đại số - Chương 6 Toán 7 Cánh diều ============ Câu hỏi khởi động trang 47 SGK Toán 7 Cánh diều tập 2 - CD Trong giờ học môn Mĩ thuật, bạn Hạnh dán lên trang vở hai hình vuông có kích thước lần lượt là 3 cm và x cm như ở Hình 1. Tổng diện tích của hai hình vuông đó là \({x^2} + 9(c{m^2})\). Biểu thức đại số \({x^2} + 9\)có gì … [Đọc thêm...] vềGiải bài 2 Đa thức một biến, nghiệm của đa thức một biến – Chương 6 Toán 7 Cánh diều

Giải SBT Cuối chương 1 (Toán 7 Chân trời)

Ngày Thuộc chủ đề:Giải sách bài tập toán 7 - Chân trời Tag với:

Giải SBT Cuối chương 1 (Toán 7 Chân trời) ============ Giải bài 1 trang 19 SBT Toán 7 Chân trời sáng tạo tập 1 Thực hiện phép tính: \(a)\dfrac{3}{7} + \dfrac{3}{7}:\left( { - \dfrac{3}{2}} \right) - \dfrac{1}{2}\) \(b)\,\,2\dfrac{1}{2} - {\left( { - \dfrac{1}{2}} \right)^2} + \dfrac{3}{4}\) \(c)\left( {\dfrac{3}{8} - 1,25} \right):\left( {\dfrac{3}{4} - 0,25} … [Đọc thêm...] vềGiải SBT Cuối chương 1 (Toán 7 Chân trời)

Giải bài tập Bài 4: Vị trí tương đối và góc giữa hai đường thẳng. Khoảng cách từ một điểm đến một đường thẳng (C7 – Toán 10 Cánh diều)

Ngày Thuộc chủ đề:Giải bài tập Toán 10 - Cánh diều Tag với:

Giải bài tập Bài 4: Vị trí tương đối và góc giữa hai đường thẳng. Khoảng cách từ một điểm đến một đường thẳng (C7 – Toán 10 Cánh diều) ================= Giải bài tập Bài 1 trang 86 SGK Toán 10 Cánh diều tập 2 Xét vị trí tương đối của mỗi cặp đường thẳng sau a) \({d_1}:3x + 2y--5 = 0\) và \({d_2}:x - 4y + 1 = 0\) ; b) \({d_3}:x - 2y + 3 = 0\) và \({d_4}: - {\rm{ }}2x + 4y + … [Đọc thêm...] vềGiải bài tập Bài 4: Vị trí tương đối và góc giữa hai đường thẳng. Khoảng cách từ một điểm đến một đường thẳng (C7 – Toán 10 Cánh diều)

Giải bài tập Cuối chương 3 (Kết nối)

Ngày Thuộc chủ đề:Giải bài tập Toán 10 - Kết nối Tag với:

Giải bài tập Cuối chương 3 (Kết nối) ============ Giải bài 3.12 trang 44 SGK Toán 10 Kết nối tri thức tập 1 Cho tam giác ABC có \(\widehat B = {135^o}\). Khẳng định nào sau đây là đúng? a) A. \(S = \frac{1}{2}ca\) B. \(S = \frac{{ - \sqrt 2 }}{4}ac\) C. \(S = \frac{{\sqrt 2 }}{4}bc\) D. \(S = \frac{{\sqrt 2 }}{4}ca\) b) A. \(R = \frac{a}{{\sin … [Đọc thêm...] vềGiải bài tập Cuối chương 3 (Kết nối)

Giải bài tập Ôn tập – Chương 7 (Chân trời)

Ngày Thuộc chủ đề:Giải bài tập Toán 10 – Chân trời Tag với:

Giải bài tập Ôn tập - Chương 7 (Chân trời) ===========   Giải bài 1 trang 18 SGK Toán 10 Chân trời sáng tạo tập 2 Xét dấu của các tam thức bậc hai sau: a) \(f\left( x \right) = 6{x^2} + 41x + 44\) b) \(g\left( x \right) =  - 3{x^2} + x - 1\) c) \(h\left( x \right) = 9{x^2} + 12x + 4\)   Phương pháp giải Bước 1: Tính và xác định dấu của biệt … [Đọc thêm...] vềGiải bài tập Ôn tập – Chương 7 (Chân trời)

Giải bài tập Bài 2: Giải bất phương trình bậc hai một ẩn (Chân trời)

Ngày Thuộc chủ đề:Giải bài tập Toán 10 – Chân trời Tag với:

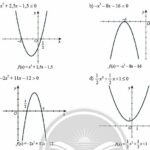
Giải bài tập Bài 2: Giải bất phương trình bậc hai một ẩn (Chân trời) ========= Giải bài 1 trang 12 SGK Toán 10 Chân trời sáng tạo tập 2 Dựa vào đồ thị của hàm số bậc hai tương ứng, hãy xác định tập nghiệm của các bất phương trình bậc hai sau đây:   Phương pháp giải +) Phần đồ thị nằm trên trục hoành có các x tương ứng là nghiệm của BPT \(f\left( x … [Đọc thêm...] vềGiải bài tập Bài 2: Giải bất phương trình bậc hai một ẩn (Chân trời)

Bài tập cuối Chương 2 – Giải SBT Toán 6 – Sách Chân trời

Ngày Thuộc chủ đề:Giải sách bài tập Toán 6 – Chân trời Tag với:

Bài tập cuối Chương 2 - Giải SBT Toán lớp 6 - Sách Chân trời sáng tạo ============ Thuộc [Sách chân trời] Giải SBT Toán 6 ============= Bài 1. Tính: a) 173 - (12 - 29); b) (-255) - (77 - 22) c) (-66).5 d) (-340).(-300) Lời giải a) 173 - (12 - 29) = 190 b) (-255) - (77 - 22) = -310 c) (-66).5 = -330 d) (-340).(-300) = 102000 Bài 2. Tính: a) (-12).(-10).(-7) b) … [Đọc thêm...] vềBài tập cuối Chương 2 – Giải SBT Toán 6 – Sách Chân trời

Bài 3: Phép cộng, phép trừ các số tự nhiên – Toán lớp 6 (Tập 1) – Cánh Diều

Ngày Thuộc chủ đề:Giải bài tập Toán 6 - Cánh Diều Tag với:

Giải bài tập SGK Toán 6 - tập 1 - Sách Cánh diều - Bài 3: Phép cộng, phép trừ các số tự nhiên ============ Bài 3: Phép cộng, phép trừ các số tự nhiên Chương CHƯƠNG I. SỐ TỰ NHIÊN ============= A. GIẢI CÁC CÂU HỎI LUYỆN TẬP VẬN DỤNG Câu 1  (Trang 16 SGK Cánh Diều Toán 6 tập 1) Mẹ An mua cho An một bộ đồng phục học sinh gồm: áo sơ mi giá 125 000 đồng, áo khoác giá … [Đọc thêm...] vềBài 3: Phép cộng, phép trừ các số tự nhiên – Toán lớp 6 (Tập 1) – Cánh Diều

26. Cho hình chóp \(S.ABCD\), \(ABCD\) là hình bình hành. \(G\) là trọng tâm của tam giác \(ABC\) và \(I\) là trung điểm của \(SG\). Mặt phẳng \(\left( {ICD} \right)\) chia khối chóp \(S.ABCD\) thành hai khối. Gọi \({V_1}\) là thể tích khối chứa điểm \(S\), \({V_2}\) là thể tích khối còn lại. Tính \(\frac{{{V_1}}}{{{V_2}}}\).

Ngày Thuộc chủ đề:Trắc nghiệm Khoảng cách và góc trong không gian Tag với:,

DẠNG TOÁN TỔNG HỢP HÌNH HỌC KHÔNG GIAN - GÓC - KHOẢNG CÁCH - THỂ TÍCH - TỶ SỐ - CỰC TRỊ HÌNH HỌC =============== 26. Cho hình chóp \(S.ABCD\), \(ABCD\) là hình bình hành. \(G\) là trọng tâm của tam giác \(ABC\) và \(I\) là trung điểm của \(SG\). Mặt phẳng \(\left( {ICD} \right)\) chia khối chóp \(S.ABCD\) thành hai khối. Gọi \({V_1}\) là thể tích khối chứa điểm … [Đọc thêm...] về26. Cho hình chóp \(S.ABCD\), \(ABCD\) là hình bình hành. \(G\) là trọng tâm của tam giác \(ABC\) và \(I\) là trung điểm của \(SG\). Mặt phẳng \(\left( {ICD} \right)\) chia khối chóp \(S.ABCD\) thành hai khối. Gọi \({V_1}\) là thể tích khối chứa điểm \(S\), \({V_2}\) là thể tích khối còn lại. Tính \(\frac{{{V_1}}}{{{V_2}}}\).

Cho một khối đồ chơi có dạng khối nón, chiều cao bằng \(30cm\), trong đó có chứa một lượng nước. Nếu đặt khối đồ chơi theo hình \({H_1}\) thì chiều cao lượng nước bằng \(\frac{2}{3}\) chiều cao của khối nón. Hỏi nếu đặt khối đồ chơi theo hình \({H_2}\) thì chiều cao \(h’\)của lượng nước trong khối đó gần với giá trị nào sau đay (biết rằng trong cả hai hình vẽ nói trên thì trục của khối nón luôn vuông góc với mặt phẳng chứa mặt thoáng của nước có trong khối đồ chơi)

Ngày Thuộc chủ đề:Trắc nghiệm Khối tròn xoay Tag với:, ,

DẠNG TOÁN KHỐI TRÒN XOAY BÀI TOÁN THỰC TẾ - THỂ TÍCH HÌNH TRÒN XOAY – phát triển theo đề tham khảo Toán 2021   ĐỀ BÀI: Cho một khối đồ chơi có dạng khối nón, chiều cao bằng \(30cm\), trong đó có chứa một lượng nước. Nếu đặt khối đồ chơi theo hình \({H_1}\) thì chiều cao lượng nước bằng \(\frac{2}{3}\) chiều cao của khối nón. Hỏi nếu đặt khối đồ chơi theo … [Đọc thêm...] vềCho một khối đồ chơi có dạng khối nón, chiều cao bằng \(30cm\), trong đó có chứa một lượng nước. Nếu đặt khối đồ chơi theo hình \({H_1}\) thì chiều cao lượng nước bằng \(\frac{2}{3}\) chiều cao của khối nón. Hỏi nếu đặt khối đồ chơi theo hình \({H_2}\) thì chiều cao \(h’\)của lượng nước trong khối đó gần với giá trị nào sau đay (biết rằng trong cả hai hình vẽ nói trên thì trục của khối nón luôn vuông góc với mặt phẳng chứa mặt thoáng của nước có trong khối đồ chơi)