Giải bài tập Ôn tập – Chương 7 (Chân trời)

Giải bài tập Ôn tập – Chương 7 (Chân trời)

===========

 

Giải bài 1 trang 18 SGK Toán 10 Chân trời sáng tạo tập 2

Xét dấu của các tam thức bậc hai sau:

a) \(f\left( x \right) = 6{x^2} + 41x + 44\)

b) \(g\left( x \right) =  – 3{x^2} + x – 1\)

c) \(h\left( x \right) = 9{x^2} + 12x + 4\)

 

Phương pháp giải

Bước 1: Tính và xác định dấu của biệt thức \(\Delta  = {b^2} – 4ac\)

Bước 2: Xác định nghiệm của \(f\left( x \right)\)nếu có

Bước 3: Các định dấu của hệ số a

Bước 4: Xác định dấu của \(f\left( x \right)\)

Lời giải chi tiết

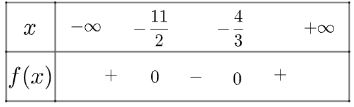
a) \(f\left( x \right) = 6{x^2} + 41x + 44\) có \(\Delta  = 625 > 0\), có hai nghiệm phân biệt là \({x_1} =  – \frac{{11}}{2},{x_2} =  – \frac{4}{3}\) và có \(a = 6 > 0\)

Ta có bảng xét dấu \(f\left( x \right)\)như sau:

Vậy \(f\left( x \right)\) dương trong khoảng \(\left( { – \infty ; – \frac{{11}}{2}} \right) \cup \left( { – \frac{4}{3}; + \infty } \right)\) và âm trong khoảng \(\left( { – \frac{{11}}{2}; – \frac{4}{3}} \right)\)

b) \(g\left( x \right) =  – 3{x^2} + x – 1\) có \(\Delta  =  – 11 < 0\) và có \(a =  – 3 < 0\)

Ta có bảng xét dấu như sau

Vậy \(g\left( x \right)\)luôn âm với mọi \(x \in \mathbb{R}\)

c) \(h\left( x \right) = 9{x^2} + 12x + 4\) có \(\Delta  = 0\), có nghiệm kép là \({x_1} = {x_2} =  – \frac{2}{3}\) và có \(a = 9 > 0\)

Ta có bảng xét dấu của \(h\left( x \right)\) như sau:

Vậy \(h\left( x \right)\) luôn dương khi \(x \ne  – \frac{2}{3}\)

Giải bài 2 trang 18 SGK Toán 10 Chân trời sáng tạo tập 2

Giải các bất phương trình sau:

a) \(7{x^2} – 19x – 6 \ge 0\)

b) \( – 6{x^2} + 11x > 10\)

c) \(3{x^2} – 4x + 7 > {x^2} + 2x + 1\)

d) \({x^2} – 10x + 25 \le 0\)

 

Phương pháp giải

Bước 1: Tính và xác định dấu của biệt thức \(\Delta  = {b^2} – 4ac\)

Bước 2: Xác định nghiệm của \(f\left( x \right)\)nếu có

Bước 3: Các định dấu của hệ số a

Bước 4: Xác định dấu của \(f\left( x \right)\)

Lời giải chi tiết

a) Xét tam thức \(f\left( x \right) = 7{x^2} – 19x – 6\) có \(\Delta  = 529 > 0\), có hai nghiệm phân biệt \({x_1} =  – \frac{2}{7},{x_2} = 3\) và có \(a = 7 > 0\)

Ta có bảng xét dấu như sau

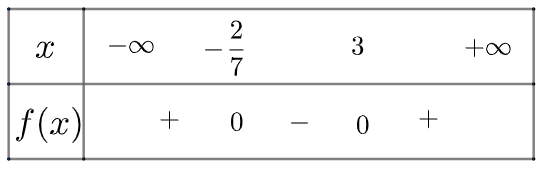
Vậy nghiệm của bất phương trình là đoạn \(\left[ { – \frac{2}{7};3} \right]\)

b) \( – 6{x^2} + 11x > 10 \Leftrightarrow  – 6{x^2} + 11x – 10 > 0\)

Xét tam thức \(f\left( x \right) =  – 6{x^2} + 11x – 10\) có \(\Delta  =  – 119 < 0\)và có \(a =  – 6 < 0\)

Ta có bảng xét dấu như sau

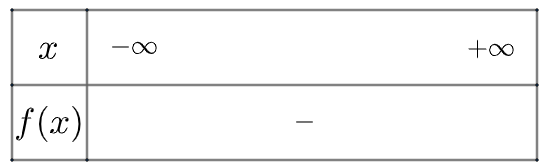
Vậy bất phương trình vô nghiệm

c) \(3{x^2} – 4x + 7 > {x^2} + 2x + 1 \Leftrightarrow 2{x^2} – 6x + 6 > 0\)

Xét tam thức \(f\left( x \right) = 2{x^2} – 6x + 6\) có \(\Delta  =  – 12 < 0\)và có \(a = 2 > 0\)

Ta có bảng xét dấu như sau

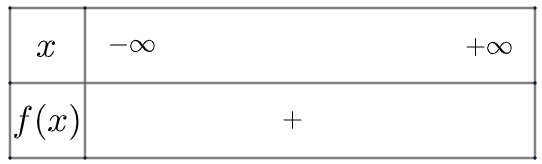
Vậy bất phương trình có vô số nghiệm

d) Xét tam thức \(f\left( x \right) = {x^2} – 10x + 25\) có \(\Delta  = 0\), có nghiệm kép \({x_1} = {x_2} = 5\) và có \(a = 1 > 0\)

Ta có bảng xét dấu như sau

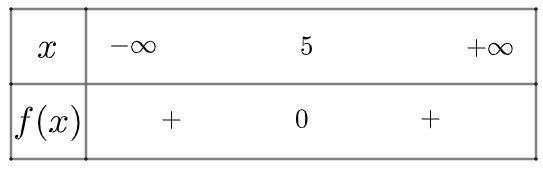
Vậy nghiệm của bất phương trình là \(x = 5\)

Giải bài 3 trang 18 SGK Toán 10 Chân trời sáng tạo tập 2

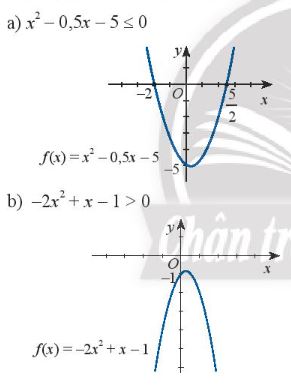
Dựa vào đồ thị của hàm số bậc hai được cho, hãy giải các bất phương trình sau:

 

 

Phương pháp giải

Quan sát vào đồ thị ta thấy

+) Tại giao điểm của đồ thị và trục hoành là nghiệm của \(f\left( x \right) = 0\)

+) Khoảng của x mà phần độ thị nằm trên trục hoành là nghiệm của \(f\left( x \right) > 0\)

+) Khoảng của x mà phần độ thị nằm dưới trục hoành là nghiệm của \(f\left( x \right) < 0\)

Lời giải chi tiết

a) Quan sát vào độ thị ta thấy đoạn mà đồ thị nằm dưới truch hoành là \(\left[ { – 2;\frac{5}{2}} \right]\)

Vậy nghiệm của bất phương trình \({x^2} – 0,5x – 5 \le 0\) là đoạn  \(\left[ { – 2;\frac{5}{2}} \right]\)

b) Quan sát vào đồ thị ta thấy đồ thị luôn nằm dưới trục hoành

Vậy nghiệm của bất phương trình \( – 2{x^2} + x – 1 > 0\) vô nghiệm

Giải bài 4 trang 18 SGK Toán 10 Chân trời sáng tạo tập 2

Giải các phương trình sau:

a) \(\sqrt {{x^2} – 7x}  = \sqrt { – 9{x^2} – 8x + 3} \)

b) \(\sqrt {{x^2} + x + 8}  – \sqrt {{x^2} + 4x + 1}  = 0\)

c) \(\sqrt {4{x^2} + x – 1}  = x + 1\)

d) \(\sqrt {2{x^2} – 10x – 29}  = \sqrt {x – 8} \)

 

Phương pháp giải

Bước 1: Bình phương hai vế để làm mất dấu căn, chuyển vế và rút gọn

Bước 2: Giải phương trình bậc hai vừa nhân được

Bước 3: Thử lại nghiệm vừa tìm được và kết luận

Lời giải chi tiết

a) \(\sqrt {{x^2} – 7x}  = \sqrt { – 9{x^2} – 8x + 3} \)

\(\begin{array}{l} \Rightarrow {x^2} – 7x =  – 9{x^2} – 8x + 3\\ \Rightarrow 10{x^2} + x – 3 = 0\end{array}\)

\( \Rightarrow x =  – \frac{3}{5}\) và \(x = \frac{1}{2}\)

Thay hai nghiệm vừa tìm được vào phương trình \(\sqrt {{x^2} – 7x}  = \sqrt { – 9{x^2} – 8x + 3} \) thì ta thấy chỉ có nghiệm \(x =  – \frac{3}{5}\) thỏa mãn phương trình

Vậy nghiệm của phương trình là \(x =  – \frac{3}{5}\)

b) \(\sqrt {{x^2} + x + 8}  – \sqrt {{x^2} + 4x + 1}  = 0\)

\(\begin{array}{l} \Rightarrow \sqrt {{x^2} + x + 8}  = \sqrt {{x^2} + 4x + 1} \\ \Rightarrow {x^2} + x + 8 = {x^2} + 4x + 1\\ \Rightarrow 3x = 7\\ \Rightarrow x = \frac{7}{3}\end{array}\)

Thay \(x = \frac{7}{3}\) vào phương trình \(\sqrt {{x^2} + x + 8}  – \sqrt {{x^2} + 4x + 1}  = 0\) ta thấy thỏa mãn phương trình

Vậy nghiệm của phương trình đã cho là \(x = \frac{7}{3}\)

c) \(\sqrt {4{x^2} + x – 1}  = x + 1\)

\(\begin{array}{l} \Rightarrow 4{x^2} + x – 1 = {\left( {x + 1} \right)^2}\\ \Rightarrow 4{x^2} + x – 1 = {x^2} + 2x + 1\\ \Rightarrow 3{x^2} – x – 2 = 0\end{array}\)

\( \Rightarrow x =  – \frac{2}{3}\) và \(x = 1\)

Thay hai nghiệm trên vào phương trình \(\sqrt {4{x^2} + x – 1}  = x + 1\) ta thấy cả hai nghiệm đều thỏa mãn

Vậy nghiệm của phương trình trên là \(x =  – \frac{2}{3}\) và \(x = 1\)

d) \(\sqrt {2{x^2} – 10x – 29}  = \sqrt {x – 8} \)

\(\begin{array}{l} \Rightarrow 2{x^2} – 10x – 29 = x – 8\\ \Rightarrow 2{x^2} – 11x – 21 = 0\end{array}\)

\( \Rightarrow x =  – \frac{3}{2}\) và \(x = 7\)

Thay hai nghiệm \(x =  – \frac{3}{2}\) và \(x = 7\) vào phương trình  \(\sqrt {2{x^2} – 10x – 29}  = \sqrt {x – 8} \) ta thấy cả hai đều không thảo mãn phương trình

Vậy phương trình \(\sqrt {2{x^2} – 10x – 29}  = \sqrt {x – 8} \) vô nghiệm

Giải bài 5 trang 18 SGK Toán 10 Chân trời sáng tạo tập 2

Một tam giác vuông có một cạnh góc vuông ngắn hơn cạnh huyền 8 cm. Tính độ dài của cạnh huyền, biết chu vi của tam giác bằng 30 cm.

Phương pháp giải

Bước 1: Đặc cạnh huyền của tam giác là x (\(x > 8\)), xác định các cạnh còn lại qua mối quan hệ với cạnh huyền

Bước 2: Lập phương trình từ giả thiết chu vi biết chu vi được tính bằng công thức \(C = a + b + c\)

Bước 3: Giải phương trình vừa tìm được.

Lời giải chi tiết

Đặt cạnh huyền của tam giác là x (\(x > 8\))

Theo giải thiết ta tính được cạnh góc vuông là \(x – 8\)

Áp dụng định lý Pitago ta tính được cạnh góc vuông còn lại là \(\sqrt {{x^2} – {{\left( {x – 8} \right)}^2}}  = \sqrt {16x – 64} \)

Ta có chu vi của tam giác là \(x + \left( {x – 8} \right) + \sqrt {16x – 64}  = 30\)

\(\begin{array}{l} \Leftrightarrow \sqrt {16x – 64}  = 38 – 2x\\ \Rightarrow 16x – 64 = {\left( {38 – 2x} \right)^2}\\ \Rightarrow 16x – 64 = 1444 – 152x + 4{x^2}\\ \Rightarrow 4{x^2} – 168x + 1508 = 0\end{array}\)

\( \Rightarrow x = 13\) và \(x = 29\)

Thay \(x = 13\) và \(x = 29\) vào phương trình \(\sqrt {16x – 64}  = 38 – 2x\) ta thấy chỉ có \(x = 13\) thảo mãn phương trình

Vậy cạnh huyền có độ dài là 13 cm.

Giải bài 6 trang 18 SGK Toán 10 Chân trời sáng tạo tập 2

Một quả bóng được bắn thẳng lên từ độ cao 2 m với vận tốc ban đầu là 30 m/s. Khoảng cách quả bóng so với mặt đất t giây được cho bởi hàm số: \(h\left( t \right) =  – 4,9{t^2} + 30t + 2\)  với \(h\left( t \right)\) tính bằng đơn vị mét. Hỏi quả bóng nằm ở độ cao trên 40 m trong thời gian bao lâu? Làm tròn kết quả đến hàng phần mười.

 

Phương pháp giải

Bước 1: Từ giả thiết lập bất phương trình.

Bước 2: Giải bất phương trình vừa tìm được.

Lời giải chi tiết

Theo giả thiết, khoảng thời gian bóng nằm ở độ cao 40 m là nghiệm của bất phương trình sau:

\(\begin{array}{l}h\left( t \right) > 40 \Leftrightarrow  – 4,9{t^2} + 30t + 2 > 40\\ \Leftrightarrow  – 4,9{t^2} + 30t – 38 > 0\end{array}\)

Xét tam thức \(f\left( t \right) =  – 4,9{t^2} + 30t – 38\) có \(\Delta  = 155,2 > 0\), có hai nghiệm phân biệt là \({x_1} \simeq 1,8;{x_2} \simeq 4,3\) và có \(a =  – 4,9 < 0\)

Ta có bảng xét dấu như sau:

Từ đó cho thấy khoảng từ 1,8 s đến 4,3 s lag khoảng thời gian bóng cao so với mặt đất lớn hơn 40 m

Vậy quả bóng nằm ở độ cao trên 40 m trong thời gian 2,5 giây.

Giải bài 7 trang 18 SGK Toán 10 Chân trời sáng tạo tập 2 – CTST

Một chú cá heo nhảy lên khỏi mặt nước sau t giây được cho bởi hàm số \(h(t)=−4,9t^2+9,6t\) Tính khoảng thời gian cá heo ở trên không.

 

Phương pháp giải

Bước 1: Từ giả thiết lập bất phương trình

Bước 2: Giải bất phương trình vừa tìm được

Lời giải chi tiết

Khoảng thời gian cá heo ở trên không chính khoảng cá heo cao hơn mặt nước

Ta có bất phương trình \(h\left( t \right) > 0 \Leftrightarrow  – 4,9{t^2} + 9,6t > 0\)

Xét tam thức \(f\left( t \right) =  – 4,9{t^2} + 9,6t\) có \(\Delta  = 92.16 > 0\), có hai nghiệm phân biệt là \({x_1} = 0,{x_2} = \frac{{96}}{{49}}\) và có \(a =  – 4,9 < 0\)

Ta có bảng xét dấu như sau:

Vậy khoảng thời gian cá heo ở trên không là khoảng \(\left( {0;\frac{{96}}{{49}}} \right)\) giây

Giải bài 8 trang 18 SGK Toán 10 Chân trời sáng tạo tập 2

Lợi nhuận một tháng p(x) của một quán ăn phụ thuộc vào giá trung bình x của các món ăn theo công thức \(p(x)=−30x^2+2100x−15000\), với đơn vị tính bằng nghìn đồng. Nếu muốn lợi nhuận không dưới 15 triệu đồng một tháng thì giá bán trung bình của các món ăn cần nằm trong khoảng nào?

Phương pháp giải

Bước 1: Từ giả thiết lập bất phương trình

Bước 2: Giải bất phương trình vừa tìm được

Lời giải chi tiết

15 triệu đồng = 15000 nghìn đồng

Từ giả thiết bài toán ta có bất phương trình \(p\left( x \right) \ge 15000 \Leftrightarrow  – 30{x^2} + 2100x – 15000 \ge 15000\)

\( \Rightarrow  – 30{x^2} + 2100x – 30000 \ge 0\)

Xét tam thức \(f\left( x \right) =  – 30{x^2} + 2100x – 30000\) có \(\Delta  = 810000 > 0\), có hai nghiệm phân biệt là \({x_1} = 20,{x_2} = 50\) và \(a =  – 30 < 0\)

Ta có bảng xét dấu như sau

Nếu muốn lợi nhuận không dưới 15 triệu đồng một tháng thì giá bán trung bình của các món ăn cần nằm trong khoảng 20 đến 50 nghìn đồng.

Giải bài 9 trang 18 SGK Toán 10 Chân trời sáng tạo tập 2

Quỹ đạo của một quả bóng được mô tả bằng hàm số \(y=f(x)=−0,03x^2+0,4x+1,5\) với y (tính bằng mét) là độ cao của quả bóng so với mặt đất khi độ dịch chuyển theo phương ngang của bóng là x (tính bằng mét). Để quả bóng có thể ném được qua lưới cao 2 m, người ta phải đứng cách lưới bao xa? Làm tròn kết quả đến hàng phần mười

 

Phương pháp giải

Bước 1: Từ giả thiết lập bất phương trình

Bước 2: Giải bất phương trình vừa tìm được

Lời giải chi tiết

Để quả bóng có thể ném được qua lưới cao 2 m thì \(y = f\left( x \right) =  – 0,03{x^2} + 0,4x + 1,5 > 2\)

\( \Rightarrow f\left( x \right) =  – 0,03{x^2} + 0,4x – 0,5 > 0\)

Xét tam thức \(f\left( x \right) =  – 0,03{x^2} + 0,4x – 0,5\) có \(\Delta  = 0,1 > 0\), có hai nghiệm phân biệt là \({x_1} \simeq 1,4;{x_2} \simeq 11,9\) và có \(a =  – 0,03 < 0\)

Ta có bảng xét dấu như sau

Vậy để quả bóng có thể ném được qua lưới cao 2 m, người ta phải đứng cách lưới từ 1,4 cho đến 11,9 mét