Giải bài tập Bài 1: Dấu của tam thức bậc hai (Chân trời)
==========
Giải bài 1 trang 9 SGK Toán 10 Chân trời sáng tạo tập 2
Đa thức nào sau đây là tam thức bậc hai?
a) \(4{x^2} + 3x + 1\)
b) \({x^3} + 3{x^2} – 1\)
c) \(2{x^2} + 4x – 1\)
Phương pháp giải
Đa thức bậc hai \(f\left( x \right) = a{x^2} + bx + c\) với a, b, c là hệ số, \(a \ne 0\) và x là biến số được gọi là tam thức bậc hai.
Lời giải chi tiết
a) Đa thức \(4{x^2} + 3x + 1\) là tam thức bậc hai
b) Đa thức \({x^3} + 3{x^2} – 1\) không là tam thức bậc hai
c) Đa thức \(2{x^2} + 4x – 1\) là tam thức bậc hai
Giải bài 2 trang 9 SGK Toán 10 Chân trời sáng tạo tập 2
Xác định giá trị của m để các đa thức sau là tam thức bậc hai
a) \(\left( {m + 1} \right){x^2} + 2x + m\)
b) \(m{x^3} + 2{x^2} – x + m\)
c) \( – 5{x^2} + 2x – m + 1\)
Phương pháp giải
Bước 1: Xác định \(a\) là hệ số của \({x^2}\)
Bước 2: Đa thức \(a{x^2} + bx + c\)được gọi là tam thức bậc hai khi \(a \ne 0\)
Lời giải chi tiết
a) Ta có: \(a = m + 1\)
Để đa thức \(\left( {m + 1} \right){x^2} + 2x + m\) là tam thức bậc hai khi và chỉ khi \(m + 1 \ne 0\)
\( \Leftrightarrow m \ne – 1\)
Vậy khi \(m \ne – 1\) thì đa thức \(\left( {m + 1} \right){x^2} + 2x + m\)là tam thức bậc hai
b) Ta có: \(a = 2\)
Để đa thức \(m{x^3} + 2{x^2} – x + m\) là tam thức bậc hai khi và chỉ khi \(m = 0\)
Vậy khi \(m = 0\) thì đa thức \(m{x^3} + 2{x^2} – x + m\)là tam thức bậc hai
c) Ta có \(a = – 5\)
Hệ số c không ảnh hưởng đến tam thức bậc hai
Vậy đa thức \( – 5{x^2} + 2x – m + 1\) là tam thức bậc hai với mọi m
Giải bài 3 trang 10 SGK Toán 10 Chân trời sáng tạo tập 2
Dựa vào đồ thị của các hàm số bậc hai sau đây, hãy lập bảng xét dấu của tam thức bậc hai tương ứng

Phương pháp giải
Bước 1: Xác định nghiệm của tam thức (là giao điểm của đồ thị với trục hoành)
Bước 2: Xác định khoảng mà \(f\left( x \right) > 0\) (khoảng đồ thị nằm trên trục hoành)
Bước 3: Xác định khoảng mà \(f\left( x \right) < 0\) (khoảng đồ thị nằm dưới trục hoành)
Bước 4: Lập bảng xét dấu
Lời giải chi tiết
a) Tam thức \(f\left( x \right) = {x^2} + 1,5x – 1\) có hai nghiệm phân biệt \({x_1} = – 2;{x_2} = \frac{1}{2}\)
\(\)\(f\left( x \right) > 0\) khi \(x \in \left( { – \infty , – 2} \right) \cup \left( {\frac{1}{2}, + \infty } \right)\) và \(f\left( x \right) < 0\) khi \(x \in \left( { – 2,\frac{1}{2}} \right)\)
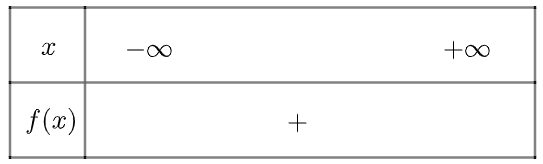
Ta có bảng xét dấu như sau
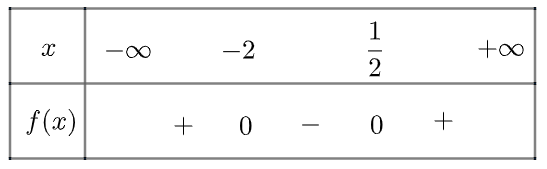
b) Tam thức \(g\left( x \right) = {x^2} + x + 1\) vô nghiệm, \(g\left( x \right) > 0\forall x \in \mathbb{R}\)
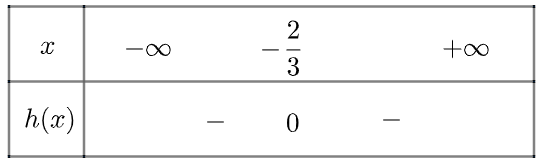
Ta có bảng xét dấu như sau
c) Tam thức \(h\left( x \right) = – 9{x^2} – 12x – 4\) có nghiệm kép \({x_1} = {x_2} = – \frac{2}{3}\) và \(h\left( x \right) < 0\forall x \ne – \frac{2}{3}\)
Ta có bảng xét dấu như sau
d) Tam thức \(f\left( x \right) = – 0,5{x^2} + 3x – 6\) vô nghiệm và \(f\left( x \right) < 0\forall x \in \mathbb{R}\)
Ta có bảng xét dấu như sau:

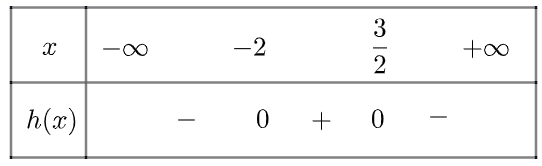
e) Tam thức \(g\left( x \right) = – {x^2} – 0,5x + 3\) có hai nghiệm \({x_1} = – 2,{x_2} = \frac{3}{2}\)
\(g\left( x \right) > 0\) khi \(x \in \left( { – 2,\frac{3}{2}} \right)\) và \(g\left( x \right) < 0\) khi \(x \in \left( { – \infty , – 2} \right) \cup \left( {\frac{3}{2}, + \infty } \right)\)
Ta có bảng xét dấu như
g) Tam thức \(h\left( x \right) = {x^2} + 2\sqrt 2 x + 2\) có nghiệm kép \({x_1} = {x_2} = – \sqrt 2 \)
\(h\left( x \right) > 0\forall x \ne – \sqrt 2 \)
Ta có bảng xét dấu như sau

Giải bài 4 trang 10 SGK Toán 10 Chân trời sáng tạo tập 2
Xét dấu của các tam thức bậc hai sau đây:
a) \(f\left( x \right) = 2{x^2} + 4x + 2\)
b) \(f\left( x \right) = – 3{x^2} + 2x + 21\)
c) \(f\left( x \right) = – 2{x^2} + x – 2\)
d) \(f\left( x \right) = – 4x(x + 3) – 9\)
e) \(f\left( x \right) = \left( {2x + 5} \right)\left( {x – 3} \right)\)
Phương pháp giải
Bước 1: Tính và xác định dấu của biệt thức \(\Delta = {b^2} – 4ac\)
Bước 2: Xác định nghiệm của \(f\left( x \right)\) (nếu có) \(x = \frac{{ – b \pm \sqrt {{b^2} – 4ac} }}{{2a}}\)
Bước 3: Xác định dấu của hệ số \(a\)
Bước 4: Xác định dấu của \(f\left( x \right)\)
Lời giải chi tiết
a) \(f\left( x \right) = 2{x^2} + 4x + 2\) có \(\Delta = 0\), có nghiệm kép là \({x_1} = {x_2} = – 1\)
và \(a = 2 > 0\)
Ta có bảng xét dấu như sau:
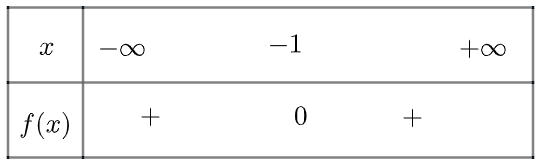
Vậy \(f\left( x \right)\) dương với mọi \(x \ne – 1\)
b) \(f\left( x \right) = – 3{x^2} + 2x + 21\) có \(\Delta = 256 > 0\), hai nghiệm phân biệt là \({x_1} = – \frac{7}{3};{x_2} = 3\)
và \(a = – 3 < 0\)
Ta có bảng xét dấu như sau:
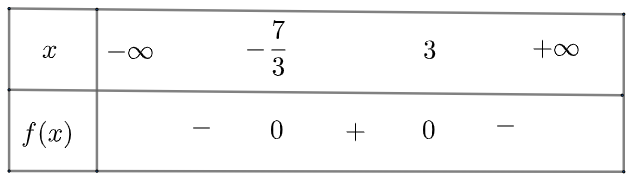
Vậy \(f\left( x \right)\) dương với \(x \in \left( { – \frac{7}{3};3} \right)\) và âm khi \(x \in \left( { – \infty ; – \frac{7}{3}} \right) \cup \left( {3; + \infty } \right)\)
c) \(f\left( x \right) = – 2{x^2} + x – 2\) có \(\Delta = – 15 < 0\), tam thức vô nghiệm
và \(a = – 2 < 0\)
Ta có bảng xét dấu như sau:

Vậy \(f\left( x \right)\) âm với mọi \(x \in \mathbb{R}\)
d) \(f\left( x \right) = – 4x\left( {x + 3} \right) – 9 = – 4{x^2} – 12x – 9\) có \(\Delta = 0\), tam thức có nghiệm kép \({x_1} = {x_2} = – \frac{3}{2}\) và \(a = – 4 < 0\)
Ta có bảng xét dấu như sau
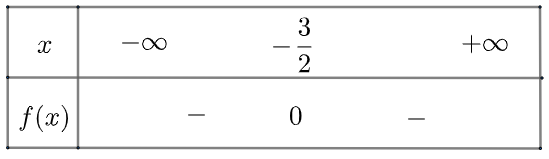
Vậy \(f\left( x \right)\) âm với mọi \(x \ne – \frac{3}{2}\)
e) \(f\left( x \right) = \left( {2x + 5} \right)\left( {x – 3} \right) = 2{x^2} – x – 15\) có \(\Delta = 121 > 0\), có hai nghiệm phân biệt \({x_1} = – \frac{5}{2};{x_2} = 3\) và có \(a = 2 > 0\)
Ta có bảng xét dấu như sau
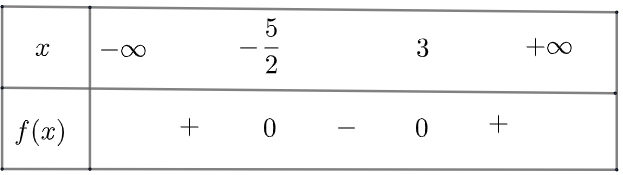
Vậy \(f\left( x \right)\) âm với \(x \in \left( { – \frac{5}{2};3} \right)\) và dương khi \(x \in \left( { – \infty ; – \frac{5}{2}} \right) \cup \left( {3; + \infty } \right)\)
Giải bài 5 trang 10 SGK Toán 10 Chân trời sáng tạo tập 2
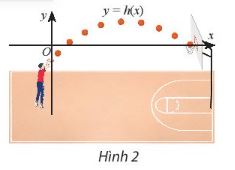
Độ cao (tính bằng mét) của một quả bóng so với vành rổ khi bóng di chuyển được x mét theo phương ngang được mô phỏng bằng hàm số \(h\left( x \right) = – 0,1{x^2} + x – 1\). Trong các khoảng nào của x thì bóng nằm: cao hơn vành rổ, thấp hơn vành rổ và ngang vành rổ? Làm tròn các kết quả đến hàng phần mười.
Phương pháp giải
Bước 1: Tính và xác định dấu của biệt thức \(\Delta = {b^2} – 4ac\)
Bước 2: Xác định nghiệm của \(h\left( x \right)\) (nếu có) \(x = \frac{{ – b \pm \sqrt {{b^2} – 4ac} }}{{2a}}\)
Bước 3: Lập bảng xét dấu
Bước 4: Dựa vào bảng xét dấu đưa ra các khoảng theo yêu cầu
+) Khoảng mà \(h\left( x \right) > 0\) là khoảng bóng nằm cao hơn vành rổ
+) Khoảng mà \(h\left( x \right) < 0\) là khoảng bóng nằm thấp hơn vành rổ
+) Khoảng mà \(h\left( x \right) = 0\) là khoảng bóng nằm ngang vành rổ
Lời giải chi tiết
\(h\left( x \right) = – 0,1{x^2} + x – 1\) có \(\Delta = \frac{3}{5} > 0\), có hai nghiệm phân biệt là \({x_1} = 5 – \sqrt {15} ;{x_2} = 5 + \sqrt {15} \)
Ta có bảng xét dấu như sau

Vậy khoảng bóng nằm trên vành rổ là \(x \in \left( {1,2;8,9} \right)\)mét
khoảng bóng nằm dưới vành rổ là \(x \in \left( { – \infty ;1,2} \right) \cup \left( {8,9; + \infty } \right)\) mét
khoảng bóng nằm ngang vành rổ là \(x \simeq \left\{ {1,2;8,9} \right\}\)
Giải bài 6 trang 10 SGK Toán 10 Chân trời sáng tạo tập 2
Một khung dây thép hình chữ nhật có chiều dài 20 cm và chiều rộng 15 cm được uốn lại thành hình chữ nhật mới có kích thước (20+x) cm và (15−x) cm. Với x nằm trong các khoảng nào thì diện tích của khung sau khi uốn: tăng lên, không thay đổi, giảm đi?
Phương pháp giải
Bước 1: Lập hiệu giữa diện tích mới và diện tích cũ \(f\left( x \right) = 20.15 – \left( {20 + x} \right)\left( {15 – x} \right)\) với \(x > 0\)
Bước 2: Tìm các khoảng thỏa mãn yêu cầu
+) Khoảng mà \(f\left( x \right) > 0\) là khoảng diện tích tăng lên
+) Khoảng mà \(f\left( x \right) < 0\) là khoảng diện tích giảm đi
+) Khoảng mà \(f\left( x \right) = 0\) là khoảng diện tích không đổi
Lời giải chi tiết
Theo giải thiết ta có tam thức sau: \(f\left( x \right) = 20.15 – \left( {20 + x} \right)\left( {15 – x} \right) = – {x^2} + 5x\)
Tam thức có \(\Delta = 25 > 0\), có hai nghiệm phân biệt \({x_1} = 0;{x_2} = 5\)
Ta có bảng xét dấu như sau

Vậy khoảng diện tích tăng lên là \(x \in \left( {0;5} \right)\), khoảng diện giảm đi là \(x > 5\) và diện tích không đổi khi \(x = 0\) và \(x = 5\)
Chú ý khi giải:
Vì x là độ dài nên điều kiện hiển nhiên của x là \(x > 0\)
Giải bài 7 trang 10 SGK Toán 10 Chân trời sáng tạo tập 2
Chứng minh rằng với mọi số thực m ta luôn có \(9m^2+2m>−3 \).
Phương pháp giải
Bước 1: Chuyển bất phương trình tương đương với \(f\left( x \right) = 9{m^2} + 2m + 3 > 0\)
Bước 2: Tính \(\Delta \) và chỉ ra dấu của \(\Delta \)âm
Bước 3: Áp dụng tính chất của tam thức bậc hai
Lời giải chi tiết
Yêu cầu bài toán tương đương chứng minh \(f\left( x \right) = 9{m^2} + 2m + 3 > 0\) với mọi m
Tam thức có \(\Delta = {2^2} – 4.9.3 = – 104 < 0\)
Áp dụng định lí về dấu của tam thức bậc hai ta có
\(\Delta < 0\) và \(a = 9 > 0\) nên \(f\left( x \right)\) cùng dấu với a với mọi m
Vậy \(f\left( x \right) = 9{m^2} + 2m + 3 > 0\) với mọi m \( \Leftrightarrow 9{m^2} + 2m > – 3\)với mọi m.
Giải bài 8 trang 10 SGK Toán 10 Chân trời sáng tạo tập 2
Tìm giá trị của m để:
a) \(2{x^2} + 3x + m + 1 > 0\) với mọi \(x \in \mathbb{R}\);
b) \(m{x^2} + 5x – 3 \le 0\) với mọi \(x \in \mathbb{R}\)
Phương pháp giải
a) Bước 1: Tính \(\Delta \) và xác định dấu của a
Bước 2: \(f\left( x \right) > 0\) với mọi \(x \in \mathbb{R}\) khi \(a > 0\) và \(\Delta < 0\)
b) Bước 1: Tính \(\Delta \) và xác định dấu của a
Bước 2: \(f\left( x \right) \le 0\) với mọi \(x \in \mathbb{R}\) khi \(a < 0\) và \(\Delta \le 0\)
Lời giải chi tiết
a) Tam thức \(2{x^2} + 3x + m + 1\) có \(\Delta = {3^2} – 4.2.\left( {m + 1} \right) = 1 – 8m\)
Vì \(a = 2 > 0\) nên để \(2{x^2} + 3x + m + 1 > 0\) với mọi \(x \in \mathbb{R}\) khi và chỉ khi \(\Delta < 0 \Leftrightarrow 1 – 8m < 0 \Leftrightarrow m > \frac{1}{8}\)
Vậy khi \(m > \frac{1}{8}\) thì \(2{x^2} + 3x + m + 1 > 0\) với mọi \(x \in \mathbb{R}\)
b) Tam thức \(m{x^2} + 5x – 3\) có \(\Delta = {5^2} – 4.m.\left( { – 3} \right) = 25 + 12m\)
Đề \(m{x^2} + 5x – 3 \le 0\) với mọi \(x \in \mathbb{R}\) khi và chỉ khi \(m < 0\) và \(\Delta = 25 + 12m \le 0 \Leftrightarrow m \le – \frac{{25}}{{12}}\)
Vậy \(m{x^2} + 5x – 3 \le 0\) với mọi \(x \in \mathbb{R}\) khi \(m \le – \frac{{25}}{{12}}\)
