Nồng độ $C$ của một hoá chất sau $t$ giờ tiêm vào cơ thể được xác định bởi công thức $C\left( t \right)=\dfrac{3t}{27+{{t}^{3}}}$ với $t\ge 0$

Nồng độ $C$ của một hoá chất sau $t$ giờ tiêm vào cơ thể được xác định bởi công thức $C\left( t \right)=\dfrac{3t}{27+{{t}^{3}}}$ với $t\ge 0$. Sau khoảng bao nhiêu giờ tiêm thì nồng độ của hoá chất trong máu là lớn nhất? (làm tròn kết quả đến hàng phần trăm)

Lời giải

Trả lời: $2,38$

Ta có $C’\left( t \right)=\dfrac{3\left( 27+{{t}^{3}} \right)-3t.3{{t}^{2}}}{{{\left( 27+{{t}^{3}} \right)}^{2}}}=\dfrac{81-6{{t}^{3}}}{{{\left( 27+{{t}^{3}} \right)}^{2}}}$.

$\left\{ \begin{array}{l}

C’\left( t \right)=0 \\

t\ge 0 \\

\end{array} \right.\Leftrightarrow t=\dfrac{3}{\sqrt[3]{2}}$.

Ta có bảng biến thiên

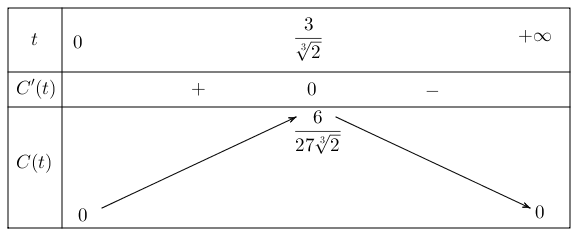
Do đó ở thời điểm $\dfrac{3}{\sqrt[3]{2}}\approx 2,38$ giờ thì nồng độ của hoá chất trong máu là lớn nhất.