Người ta muốn làm một cái bể dạng hình hộp chữ nhật không nắp (như hình vẽ)
có thể tích bằng $1{{m}^{3}}$

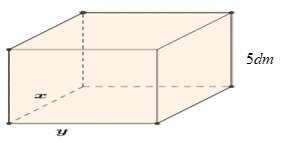
Người ta muốn làm một cái bể dạng hình hộp chữ nhật không nắp (như hình vẽ)
có thể tích bằng $1{{m}^{3}}$. Chiều cao của bể là $5dm$, các kích thước khác là $x\left( m \right)$, $y\left( m \right)$ với $x{>}0$ và $y{>}0$. Diện tích toàn phần của bể (không kể nắp) là hàm số $S\left( x \right)$ trên khoảng $\left( 0;+\infty \right)$. Đường tiệm cận xiên của đồ thị hàm số $S\left( x \right)$ là đường thẳng $y=ax+b$. Tính giá trị của biểu thức $P={{a}^{2}}+{{b}^{2}}$.
Đáp án: 5

Lời giải:

Do thể tích của bể là $1{{m}^{3}}$ nên $0,5xy=1\Leftrightarrow xy=2$
Diện tích toàn phần của bể là $S\left( x \right)=xy+2.0,5.x+2.0,5.y=2+x+\dfrac{2}{x},\left( x{>}0 \right)$
Ta có: $\lim\limits_{x\to +\infty }\left( S\left( x \right)-\left( x+2 \right) \right)=\lim\limits_{x\to +\infty }\dfrac{2}{x}=0$
Suy ra đồ thị hàm số $S\left( x \right)$ có đường tiệm cận xiên là $y=x+2$ $\Rightarrow a=1;b=2$
$P={{a}^{2}}+{{b}^{2}}=5$