Một vật chuyển động với vận tốc $v\left( \text{km/h} \right)$ phụ thuộc vào thời gian $t\left( \text{h} \right)$ có đồ thị của hàm số dạng hàm bậc ba như hình bên

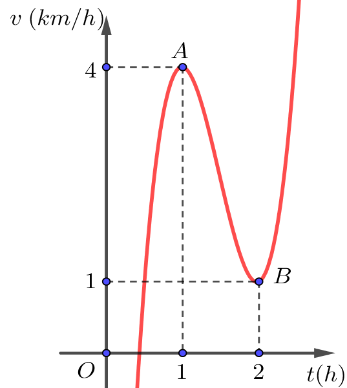
Một vật chuyển động với vận tốc $v\left( \text{km/h} \right)$ phụ thuộc vào thời gian $t\left( \text{h} \right)$ có đồ thị của hàm số dạng hàm bậc ba như hình bên. Biết rằng tại thời điểm ${{t}_{1}}=1\text{h}$ vật có vận tốc ${{v}_{1}}=4\text{km/h}$ và tại thời điểm ${{t}_{2}}=2\text{h}$ vật có vận tốc ${{v}_{2}}=1\text{km/h}$. Hỏi vận tốc của vật tại thời điểm $t=3\text{h}$ bằng bao nhiêu km/h?

Lời giải

Trả lời: 16

Giả sử hàm số vận tốc có dạng: $v\left( t \right)=a{{t}^{3}}+b{{t}^{2}}+ct+d$ (với $a\ne 0$ và $t\ge 0$ ).

Ta có: ${v}’\left( t \right)=3a{{t}^{2}}+2bt+c$.

Dựa vào đồ thị hàm số, tại các thời điểm ${{t}_{1}},{{t}_{2}}$ đồ thị hàm vận tốc đi qua các điểm cực trị $A\left( 1;4 \right),B\left( 2;1 \right)$.

Khi đó: $\left\{ \begin{array}{l}

v\left( 1 \right)=4 \\

{v}’\left( 1 \right)=0 \\

v\left( 2 \right)=1 \\

{v}’\left( 2 \right)=0 \\

\end{array} \right.\Leftrightarrow \left\{ \begin{array}{l}

a+b+c+d=4 \\

3a+2b+c=0 \\

8a+4b+2c+d=1 \\

12a+4b+c=0 \\

\end{array} \right.\Leftrightarrow \left\{ \begin{array}{l}

a=6 \\

b=-27 \\

c=36 \\

d=-11 \\

\end{array} \right.$.

Suy ra: $v\left( t \right)=6{{t}^{3}}-27{{t}^{2}}+36t-11\left( \text{km/h} \right)$.

Vậy vận tốc của vật tại thời điểm $t=3h$ là: $v\left( 3 \right)=6\cdot {{3}^{3}}-27\cdot {{3}^{2}}+36\cdot 3-11=16\text{km/h}$.