Một vật chuyển động với vận tốc $\left( m/s \right)$ được xác định bởi hàm số $f(t)=-{{t}^{3}}+3{{t}^{2}}$ với $t\ge 0$. Khi đó $f\prime (t)$ là gia tốc của vật tại thời điểm $t$ (giây). Vận tốc của vật đạt được cao nhất trong khoảng thời gian 3 giây đầu là bao nhiêu m/s?
Lời giải
Trả lời: 4
$\Rightarrow {f}’\left( t \right)=-3{{t}^{2}}+6t=0\Leftrightarrow \left[ \begin{array}{l}
t=2 \\
t=0 \\
\end{array} \right.$
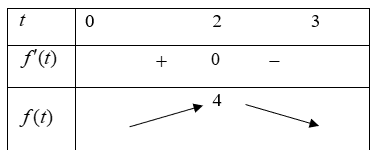
Bảng biến thiên
Vận tốc của vật đạt được cao nhất là $4m/s$