Một vận động viên đua xe F1  đang chạy với vận tốc 10 ;m/s thì anh ta tăng tốc với gia tốc a( t ) = 6t( rm( ))( (m/(s^2)) ),  trong đó t là khoảng thời gian tính bằng giây kể từ lúc tăng tốc. Hỏi quãng đường xe của anh ta đi được trong thời gian 10s kể từ lúc bắt đầu tăng tốc là bao nhiêu

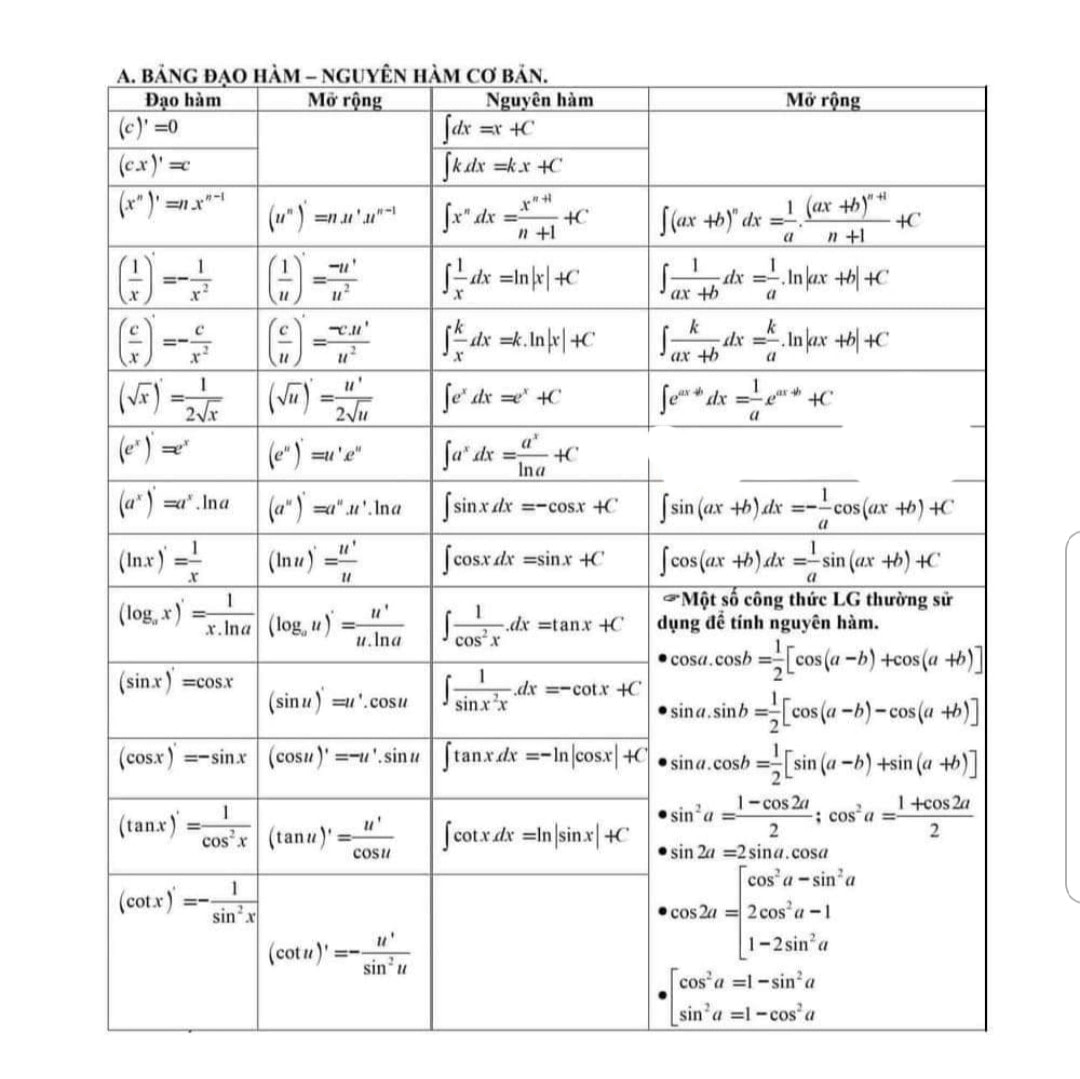
\(\begin{array}{l}
\smallint a(t)dt = \smallint 6tdt = 3{t^2} + C = v(t)\\
t = 0 \Rightarrow v = 10 \Rightarrow C = 10 \Rightarrow v(t) = 3{t^2} + 10\\
\Rightarrow S\left( t \right) = \smallint \left( {3{t^2} + 10} \right)dt = {t^3} + 10t + C
\end{array}\)

Quãng đường đi được của vật trong 10s bắt đầu từ lúc tăng tốc là:

\(
S\left( {10} \right) – S\left( 0 \right) = \left( {{{10}^3} + 10.10 + C} \right) – \left( {{0^3} + 10.0 + C} \right) = 1100{\mkern 1mu} m\)