Bài toán gốc
Một công ty trung bình bán được 1000 ti vi màn hình phẳng mỗi tuần với giá 14 triệu đồng một chiếc. Một cuộc khảo sát thị trường chỉ ra rằng, nếu cứ giảm giá bán 500 nghìn đồng trên một chiếc tivi, số lượng ti vi bán ra sẽ tăng thêm khoảng 100 ti vi mỗi tuần. Hỏi công ty nên giảm giá bao nhiêu (đơn vị triệu đồng) một chiếc ti vi cho người mua để doanh thu là lớn nhất?
Đáp án: 4,5
Lời giải: Gọi $x$ (triệu đồng) là số tiền giảm trên một chiếc ti vi, $0\le x\le 14$.
Giá một chiếc ti vi sau khi giảm giá là $14-x$ (triệu đồng).
Số lượng ti vi bán ra sau khi giảm giá là $1000+200x$ (ti vi).
Doanh thu của công ty là $\left( 1000+200x \right)\left( 14-x \right)=14000+1800x-200{{x}^{2}}$.
Xét hàm số $f\left( x \right)=14000+1800x-200{{x}^{2}},0\le x\le 14$.
Ta có ${f}’\left( x \right)=1800-400x$.
${f}’\left( x \right)=0$ $\Leftrightarrow 1800-400x=0$ $\Leftrightarrow x=4,5$.
Bảng biến thiên:
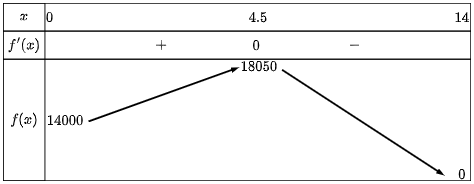
Vậy doanh thu lớn nhất là 18050 triệu đồng khi giảm $4,5$ triệu đồng một chiếc ti vi.
Phân tích và Phương pháp giải
Đây là bài toán ứng dụng thực tế tìm giá trị lớn nhất (cực trị) của hàm số, cụ thể là hàm doanh thu. Phương pháp giải là xây dựng hàm doanh thu $R(x)$ theo biến $x$ (số tiền giảm giá). Doanh thu $R(x)$ là tích của (Giá bán) nhân với (Số lượng bán được). Hàm $R(x)$ thu được là một hàm bậc hai (parabol mở xuống). Ta sử dụng đạo hàm $R'(x)$ để tìm điểm cực đại $x$ làm cho doanh thu đạt giá trị lớn nhất.
Bài toán tương tự
Một cửa hàng điện thoại trung bình bán được 2000 chiếc điện thoại thông minh mỗi tháng với giá 10 triệu đồng một chiếc. Khảo sát thị trường cho thấy, nếu cứ giảm giá bán 1 triệu đồng trên một chiếc điện thoại, số lượng bán ra sẽ tăng thêm 500 chiếc mỗi tháng. Hỏi cửa hàng nên giảm giá bao nhiêu (đơn vị triệu đồng) một chiếc điện thoại để doanh thu là lớn nhất? Đáp án: 3
Lời giải ngắn gọn:
Gọi $x$ (triệu đồng) là số tiền giảm giá trên mỗi chiếc điện thoại, $0\le x\le 10$.
Giá bán sau khi giảm giá: $10 – x$ (triệu đồng).
Số lượng điện thoại bán ra sau khi giảm giá: $2000 + 500x$ (chiếc).
Doanh thu $R(x) = (10 – x)(2000 + 500x) = 20000 + 5000x – 2000x – 500x^2 = 20000 + 3000x – 500x^2$.
Ta tìm cực trị của hàm $R(x)$:
$R'(x) = 3000 – 1000x$.
Đặt $R'(x) = 0 \Leftrightarrow 3000 – 1000x = 0 \Leftrightarrow x = 3$.
Vì $R(x)$ là hàm bậc hai có hệ số của $x^2$ âm, nên $x=3$ là điểm cực đại.
Vậy, để doanh thu lớn nhất, cửa hàng cần giảm giá 3 triệu đồng.
