Lát cắt ngang của một vùng đất ven biển được mô hình hóa thành một hàm số bậc ba $y=f\left( x \right)$ có đồ thị như hình vẽ

Bài toán gốc

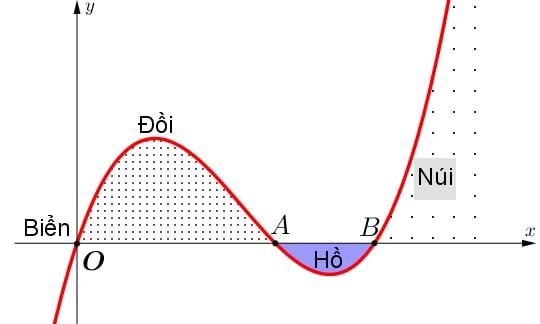
Lát cắt ngang của một vùng đất ven biển được mô hình hóa thành một hàm số bậc ba $y=f\left( x \right)$ có đồ thị như hình vẽ (đơn vị trên các trục là km). Biết khoảng cách hai bên chân đồi $OA=\dfrac{15}{8}\text{km}$, độ rộng của hồ $AB=\dfrac{9}{8}\text{km}$ và chiều cao của ngọn đồi là $243\text{m}$. Tìm độ sâu của hồ (tính theo km) tại điểm sâu nhất.
ả

Đáp án: 0,1

Lời giải: Ta có $OA=\dfrac{15}{8}\text{km}$, $OB=OA+AB=\dfrac{15}{8}+\dfrac{9}{8}=3\left( \text{km} \right)$ và chiều cao của ngọn đồi là $243\text{m}=0,243\text{km}$.
Từ hình vẽ, ta thấy đồ thị hàm số đi qua các điểm: $O\left( 0;0 \right)$, $A\left( \dfrac{15}{8};0 \right)$, $B\left( 3;0 \right)$ nên hàm số bậc ba có dạng $y=f\left( x \right)=a.x\left( x-\dfrac{15}{8} \right)\left( x-3 \right)=a\left( {{x}^{3}}-\dfrac{39}{8}{{x}^{2}}+\dfrac{45}{8}x \right)$ với $a{>}0$.
Khi đó ${y}’=a\left( 3{{x}^{2}}-\dfrac{39}{4}x+\dfrac{45}{8} \right)$; ${y}’=0\Leftrightarrow 3{{x}^{2}}-\dfrac{39}{4}x+\dfrac{45}{8}=0\Leftrightarrow \left[ \begin{array}{l} x=\dfrac{5}{2} \\ x=\dfrac{3}{4} \end{array} \right.$.
Chiều cao của ngọn đồi đạt tại điểm cực đại của đồ thị hàm số, do đó
$y\left( \dfrac{3}{4} \right)=0,243$ $\Leftrightarrow a.\dfrac{3}{4}\left( \dfrac{3}{4}-\dfrac{15}{8} \right)\left( \dfrac{3}{4}-3 \right)=0,243\Leftrightarrow a=\dfrac{16}{125}$.
Suy ra $y\left( \dfrac{5}{2} \right)=-0,1$.
Độ sâu của hồ tại điểm sâu nhất đạt tại điểm cực tiểu của đồ thị hàm số.
Vậy độ sâu của hồ tại điểm sâu nhất là $0,1\text{km}$.

Phân tích và Phương pháp giải

Đây là bài toán ứng dụng mô hình hóa thực tế bằng hàm số bậc ba. Phương pháp giải bao gồm ba bước chính: 1. Xác định dạng hàm số $y=f(x)$ dựa trên các giao điểm với trục hoành (các rễ $0, x_A, x_B$). 2. Sử dụng đạo hàm $y’$ để tìm các điểm cực trị ($x_{max}$ cho ngọn đồi và $x_{min}$ cho hồ). 3. Dựa vào giá trị cực đại (chiều cao đồi) để xác định hệ số $a$, sau đó tính giá trị cực tiểu để tìm độ sâu hồ. Cụ thể, hàm số có dạng $y=a x (x-x_A) (x-x_B)$.

Bài toán tương tự

Lát cắt ngang của một vùng đất ven biển được mô hình hóa thành một hàm số bậc ba $y=f\left( x \right)$ có đồ thị như hình vẽ (đơn vị trên các trục là km). Biết khoảng cách hai bên chân đồi $OA=\dfrac{15}{8}\text{km}$, độ rộng của hồ $AB=\dfrac{9}{8}\text{km}$ và chiều cao của ngọn đồi là $486\text{m}$. Tìm độ sâu của hồ (tính theo km) tại điểm sâu nhất.

Đáp án: 0,2 km
Lời giải ngắn gọn:
Ta có $OA=\dfrac{15}{8}\text{km}$, $OB=OA+AB=3\text{km}$. Chiều cao đồi $H = 486\text{m} = 0,486\text{km}$.
Hàm số có dạng $y=a.x\left( x-\dfrac{15}{8} \right)\left( x-3 \right)$.
Ta tìm được các điểm cực trị tại $x_{CĐ}=\dfrac{3}{4}$ và $x_{CT}=\dfrac{5}{2}$.
Giá trị cực đại (chiều cao đồi): $y\left( \dfrac{3}{4} \right)=a\cdot\dfrac{243}{128}$.
Cho $y\left( \dfrac{3}{4} \right) = 0,486 \Leftrightarrow a\cdot\dfrac{243}{128} = 0,486$. Suy ra $a = \dfrac{0,486 \cdot 128}{243} = \dfrac{256}{1000} = \dfrac{32}{125}$.
Độ sâu hồ là $|y(x_{CT})|$. Ta tính $y\left( \dfrac{5}{2} \right)=a \cdot \left( -\dfrac{25}{32} \right) = \dfrac{32}{125} \cdot \left( -\dfrac{25}{32} \right) = -\dfrac{1}{5} = -0,2$.
Vậy độ sâu của hồ tại điểm sâu nhất là $0,2\text{km}$. (Đáp án: 0,2)