Giải SBT (CTST) Bài 2: Các phép toán với đa thức nhiều biến

GIẢI CHI TIẾT SÁCH BÀI TẬP Bài 2: Các phép toán với đa thức nhiều biến – Sách CHÂN TRỜI SÁNG TẠO

================

Giải SBT Toán 8 Bài 2: Các phép toán với đa thức nhiều biến

Bài 1 trang 10 SBT Toán 8 Tập 1 : Tính:

a)$7x+(-3xy+5x)$;

b)$4x-3y-(3+3x-y)$;

c)$2xy-4xy-(y-3xy)$;

d)$(x^{2}y-3x{y}^2-y^2)+(5x{y}^2-4y^2+5x^{2}y)$.

Lời giải:

a)

$7x+(-3xy+5x)=7x-3xy+5x=(7x+5x)-3xy=12x-3xy$

b)

$4x-3y-(3+3x-y)=4x-3y-3-3x+y=(4x-3x)+(y-3y)-3=x-2y-3$

c)

$2xy-4xy-(y-3xy)=2xy-4xy-y+3xy=(2xy-4xy+3xy)-y=xy-y$

d)

$(x^{2}y-3x{y}^2-y^2)+(5x{y}^2-4y^2+5x^{2}y)=x^{2}y-3x{y}^2-y^2+5x{y}^2-4y^2+5x^{2}y$

$=(x^{2}y+5x^{2}y)+(5x{y}^2-3x{y}^2)-(y^2+4y^2)=6x^{2}y+2x{y}^2-5y^2$

Bài 2 trang 10 SBT Toán 8 Tập 1 : Tính:

a)$2a+4b+(-4b+5a)-(6a-9b)$;

b)$6a-[b+3a-(4a-b\left)\right]$.

Lời giải:

a)

$2a+4b+(-4b+5a)-(6a-9b)=2a+4b-4b+5a-6a+9b$

$=(2a+5a-6a)+(4b-4b+9b)=a+9b$

b)

$6a-[b+3a-(4a-b\left)\right]=6a-(b+3a-4a+b)=6a-2b+a$

$=(6a+a)-2b=7a-2b$

Bài 3 trang 10 SBT Toán 8 Tập 1 : Thực hiện các phép nhân:

a)$(3ab).(5bc)$;

b)$(-6a^{2}b).(-\frac{1}{2}a{b}^3)$.

Lời giải:

a)$(3ab).(5bc)=(3.5)a.(b.b)c=15a{b}^{2}c$;

b)$(-6a^{2}b).(-\frac{1}{2}a{b}^3)=[(-6\left)(-\frac{1}{2}\right)](a^2.a)(b.b^3)=3a^3{b}^4$.

Bài 4 trang 10 SBT Toán 8 Tập 1 : Thực hiện các phép nhân:

a)$(x+3y\left)(x-2y\right)$;

b)$(2x-y\left)(y-5x\right)$;

c)$(2x-5y)(y^2-2xy)$;

d)$(x-y)(x^2-xy-y^2)$.

Lời giải:

a)

$(x+3y\left)(x-2y\right)=x(x-2y)+3y(x-2y)=x^2-2xy+3xy-6y^2$

$=x^2+(3xy-2xy)-6y^2=x^2+xy-6y^2$

b)

$(2x-y\left)(y-5x\right)=2x(y-5x)-y(y-5x)=2xy-10x^2-y^2+5xy$

$=(2xy+5xy)-10x^2-y^2=7xy-10x^2-y^2$

c)

$(2x-5y\left)(y^2-2xy\right)=2x(y^2-2xy)-5y(y^2-2xy)=2x{y}^2-4x^{2}y-5y^3+10x{y}^2$

$=(2x{y}^2+10x{y}^2)-4x^{2}y-5y^3=12x{y}^2-4x^{2}y-5y^3$

d)$(x-y)(x^2-xy-y^2)=x(x^2-xy-y^2)-y(x^2-xy-y^2)$

$=x^3-x^{2}y-x{y}^2-x^{2}y+x{y}^2+y^3=x^3-(x^{2}y+x^{2}y)+(x{y}^2-x{y}^2)+y^3=x^3–2x^{2}y+y^3$

Bài 5 trang 10 SBT Toán 8 Tập 1 : Thực hiện các phép chia:

a)$24x{y}^3:(6xy)$;

b)$-3x^2{y}^{5}z:(15x{y}^3)$;

c)$(-4x^6{y}^2):(-0,1x^3{y}^2)$.

Lời giải:

a)$24x{y}^3:(6xy)=(24:6)(x:x)(y^3:y)=4y^2$;

b)$-3x^2{y}^{5}z:(15x{y}^3)=(-3:15)(x^2:x)(y^5:y^3)z=\frac{-1}{5}x{y}^{2}z$;

c)$(-4x^6{y}^2):(-0,1x^3{y}^2)=[(-4):(-0,1)](x^6:x^3)(y^2:y^2)=40x^3$.

Bài 6 trang 10 SBT Toán 8 Tập 1 : Thực hiện các phép chia:

a)$(6x^{2}y-9x{y}^2):(3xy)$;

b)$(-x{y}^2+10y):(-5y)$;

c)$(5x{y}^2+2):\frac{5}{2}$;

d)$(2x^4{y}^2-3x^2{y}^3):(-x^{2}y)$.

Lời giải:

a)$(6x^{2}y-9x{y}^2):(3xy)=6x^{2}y:(3xy)-9x{y}^2:(3xy)=2x-3y$;

b)$(-x{y}^2+10y):(-5y)=(-x{y}^2):(-5y)+10y:(-5y)=\frac{1}{5}xy-2$;

c)$(5x{y}^2+2):\frac{5}{2}=5x{y}^2:\frac{5}{2}+2:\frac{5}{2}=2x{y}^2+\frac{4}{5}$;

d)

$(2x^4{y}^2-3x^2{y}^3):(-x^{2}y)=2x^4{y}^2:(-x^{2}y)-3x^2{y}^3:(-x^{2}y)=-2x^{2}y+3y^2$

Bài 7 trang 10 SBT Toán 8 Tập 1 : Tính:

a)$3a(a-b)-b(b-3a)$;

b)$3a^2(2a+b)-2b(4a^2-b)$;

c)$(a+b\left)(a-b\right)-(a-1\left)(a-2\right)$;

d)$b(3b^2-a^3)+(a^2+3b)(ab-b^2)$.

Lời giải:

a)

$3a(a-b)-b(b-3a)=3a^2-3ab-b^2+3ab=3a^2+(3ab-3ab)-b^2=3a^2-b^2$

b)$3a^2(2a+b)-2b(4a^2-b)=6a^3+3a^{2}b-8a^{2}b+2b^2$

$=6a^3+(3a^{2}b-8a^{2}b)+2b^2=6a^3-5a^{2}b+2b^2$

c)

$(a+b\left)(a-b\right)-(a-1\left)(a-2\right)=a(a-b)+b(a-b)-a(a-2)+(a-2)$

$=a^2-ab+ab-b^2-a^2+2a+a-2=(a^2-a^2)+(ab-ab)-b^2+(2a+a)-2$

$=-b^2+3a-2$

d)

$b(3b^2-a^3)+(a^2+3b)(ab-b^2)=3b^3-a^{3}b+a^2(ab-b^2)+3b(ab-b^2)$

$=3b^3-a^{3}b+a^{3}b-a^2{b}^2+3a{b}^2-3b^3=(3b^3-3b^3)+(a^{3}b-a^{3}b)-a^2{b}^2+3a{b}^2$

$=-a^2{b}^2+3a{b}^2$

Bài 8 trang 10 SBT Toán 8 Tập 1 : Tính giá trị của đa thức:

a)$(3x-y)+(3y-x)-(x+y)$tại$x=2,7$và$y=1,3$;

b)$x(x+y)-y(x-y)$tại$x=-0,5$và$y=0,3$;

c)$(1,3x^{2}y+3,2xy+1,5y^2)-(2,2xy-1,2x^{2}y+1,5y^2)$tại$x=-2$và$y=5$.

Lời giải:

a) Ta có:$(3x-y)+(3y-x)-(x+y)=3x-y+3y-x-x-y$

$=(3x-x-x)+(3y-y-y)=x+y$

Với$x=2,7$và$y=1,3$ta có:$2,7+1,3=4$

b) Ta có:

$x(x+y)-y(x-y)=x^2+xy-xy+y^2=x^2+(xy-xy)+y^2=x^2+y^2$

Với$x=-0,5$và$y=0,3$ta có:${(}^{-0,5}2+{(}^{0,3}2=0,25+0,09=0,34$

c) Ta có:$(1,3x^{2}y+3,2xy+1,5y^2)-(2,2xy-1,2x^{2}y+1,5y^2)$

$=1,3x^{2}y+3,2xy+1,5y^2-2,2xy+1,2x^{2}y-1,5y^2$

$=(1,3x^{2}y+1,2x^{2}y)+(3,2xy-2,2xy)+(1,5y^2-1,5y^2)=2,5x^{2}y+xy$

Với$x=-2$và$y=5$ta có:$2,5.{(}^{-2}2.5+(-2).5=50-10=40$

Bài 9 trang 11 SBT Toán 8 Tập 1 : Biết rằng$x=a+b$và$y=2a-b$. Tính các đa thức sau theo a và b.

a)$A=3x-4y$;

b)$B=2xy$.

Lời giải:

a) Với$x=a+b$và$y=2a-b$thay vào A ta có:

$A=3(a+b)-4(2a-b)=3a+3b-8a+4b=(3a-8a)+(3b+4b)=-5a+7b$

b) Với$x=a+b$và$y=2a-b$thay vào B ta có:

$B=2(a+b\left)(2a-b\right)=2a(2a-b)+2b(2a-b)=4a^2-2ab+4ab-2b^2$

$=4a^2+(4ab-2ab)-2b^2=4a^2+2ab-2b^2$

Bài 10 trang 11 SBT Toán 8 Tập 1 : Từ một tấm tôn hình chữ nhật có chiều dài bằng a (cm), chiều rộng bằng b (cm), người ta cắt bỏ bốn hình vuông cạnh bằng x (cm) ở bốn góc, rồi gấp và hàn thành thùng không có nắp (Hình 1). Viết biểu thức biểu thị:

a) Thể tích nước tối đa mà thùng có thể chứa được.

b) Tổng diện tích của năm mặt của chiếc thùng.

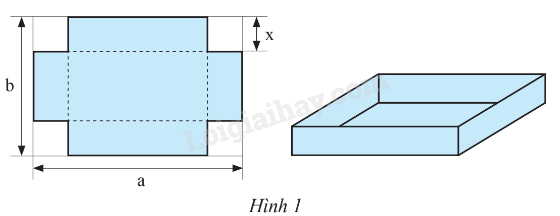
Lời giải:

Thùng trên có chiều dài là:$a-2x(cm)$, chiều rộng là$b-2x(cm)$, chiều cao là x (cm)

a) Thể tích của thùng là:

$V=(a-2x\left)(b-2x\right)x=[a(b-2x)-2x(b-2x)]x$

$=(ab-2ax-2bx+4x^2)x=abx-2a{x}^2-2b{x}^2+4x^3$

Vậy thể tích nước tối đa mà thùng có thể chứa được là$abx-2a{x}^2-2b{x}^2+4x^3(c{m}^3)$

b) Tổng diện tích năm mặt của chiếc thùng là:

$S=(a-2x\left)(b-2x\right)+2x(a-2x)+2x(b-2x)$

$=a(b-2x)-2x(b-2x)+2ax-4x^2+2bx-4x^2$

$=ab-2ax-2bx+4x^2+2ax-4x^2+2bx-4x^2$

$=ab+(2ax-2ax)+(2bx-2bx)+(4x^2-4x^2-4x^2)=ab-4x^2$

Vậy tổng diện tích của năm mặt của chiếc thùng là$ab-4x^2(c{m}^2)$

=============
THUỘC: GIẢI SÁCH BÀI TẬP MÔN TOÁN LỚP 8 – CHÂN TRỜI SÁNG TẠO