Câu hỏi:
Trong không gian cho hình chữ nhật ABCD, gọi M, N lần lượt là trung điểm của các cạnh BC và CD. Cho đa giác ABMND quay quanh trục AD ta được một khối tròn xoay \(\left( X \right).\) Tính thể tích V của khối tròn xoay \(\left( X \right)\) biết \(AB = 2cm,BC = 6cm.\)
- A. \(V = 16\pi \left( {c{m^3}} \right).\)
- B. \(V = 19\pi \left( {c{m^3}} \right).\)
- C. \(V = 33\pi \left( {c{m^3}} \right).\)
- D. \(V = 24\pi \left( {c{m^3}} \right).\)
Có vấn đề về lời giải xin các bạn để lại phản hồi cuối bài.
Đáp án đúng: B
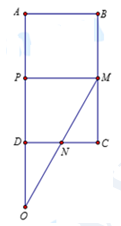
Gọi P là trung điểm của AD; \(O = MN \cap AD.\)
Thể tích khối trụ có bán kính AB và chiều cao BM là \({V_1} = \pi {.2^2}.3 = 12\pi .\)
Ta có: \(PO = 2PD = 6.\)
Thể tích khối nón đỉnh O, bán kính PM, chiều cao PO là: \({V_2} = \frac{1}{3}\pi {.2^2}.6 = 8\pi .\)
Thể tích khối nón đỉnh O, bán kính DN, chiều cao DO là: \({V_3} = \frac{1}{3}\pi {.1^2}.3 = \pi .\)
Thể tích khối tròn xoay \(\left( X \right)\) là: \(V = {V_1} + {V_2} – {V_3} = 12\pi + 8\pi – \pi = 19\pi .\)
=======
Xem thêm Lý thuyết khối tròn xoay
Bài học cùng chương bài
- Phát triển câu 8 đề tốt nghiệp THPT 2020 – Thể tích khối nón
- Câu 40: (MH Toan 2020) Cho hình nón có chiều cao bằng \(2\sqrt 5 \). Một mặt phẳng đi qua đỉnh hình nón và cắt hình nón theo một thiết diện là tam giác đều có diện tích bằng \(9\sqrt 3 \). Thể tích của khối nón được giới hạn bởi hình nón đã cho bằng
- Đề: Cho tam giác ABC đều cạnh a, đường cao AH. Tính thể tích V của khối nón sinh ra khi cho tam giác ABC quay xung quanh trục AH.
- Đề: Một chiếc ly hình nón chứa đầy rượu. Người ta uống đi một phần rượu sao cho chiều cao phần rượu còn lại bằng một nửa chiều cao ban đầu. Số phần rượu được uống là:
- Đề: Cho hình nón có bán kính đường tròn đáy là 6cm và diện tích hình tròn đáy bằng \(\frac{3}{5}\) diện tích xung quanh của hình nón. Tính thể tích V của khối nón.
- Đề: Cho khối nón có bán kính đáy 3a. Cắt khối nón đó bởi một mặt phẳng vuông góc với trục và bỏ phần trên của khối nón (phần chứa đỉnh của khối nón). Biết thiết diện là hình tròn có bán kính bằng a và độ dài phần đường sinh còn lại bằng \(\frac{{29a}}{{10}}\). Tính thể tích phần còn lại của khối nón theo a.
- Đề: Cho hình nón \(\left( N \right)\) có diện tích toàn phần bằng \(24\pi c{m^2}\) và bán kính mặt đáy bằng 3cm. Tính thể tích V của khối nón \(\left( N \right).\)
- Đề: Một que kem ốc quế gồm hai phần: phần kem có dạnh hình cầu, phần ốc quế có dạng hình nón. Giả sử hình cầu và hình nón có bán kính bằng nhau; biết rằng nếu kem tan chảy hết thì sẽ làm đầy phần ốc quế. Biết thể tích phần kem sau khi tan chảy chỉ bằng 75% thể tích kem đóng băng ban đầu. Gọi h và r lần lượt là chiều cao và bán kính của phần ốc quế. Tính tỉ số \(\frac{h}{r}.\)
- Đề: Cho hình nón có đường kính đáy bằng 6a, diện tích xung quanh bằng \(15\pi {a^2}\). Tính thể tích của khối nón.
- Đề: Tính thể tích khối nón, biết khối nón đó có chu vi đáy là \(6\pi \) và chiều cao bằng 5.
- Đề: Tính thể tích V của khối nón có chiều cao h và góc ở đỉnh bằng 900.
- Đề: Cho hình nón có bán kính đáy \(R = \sqrt 5 \) và độ dài đường sinh \(l = 3\sqrt 5 \,\). Tính thể tích V của khối nón.
- Đề: Cho lục giá đều ABCDEF có cạnh bằng 4. Cho lục giác đều đó quanh quay đường thẳng AD. Tính thể tích V của khối tròn xoay được sinh ra.
- Đề: Một hình nón có thiết diện qua trục là một tam giác cân, cạnh bên bằng 1, góc ở đỉnh bằng 1200. Thể tích khối nón bằng:
- Đề: Trong mặt phẳng cho một hình lục giác đều cạnh bằng 2. Tính thể tích của hình tròn xoay có được khi quay hình lục giác đó quanh đường thẳng đi qua hai đỉnh đối diện của nó.
Trả lời