Cho hàm số $y=\dfrac{{{x}^{2}}+3}{x-2}$ có đồ thị $(C)$

Cho hàm số $y=\dfrac{{{x}^{2}}+3}{x-2}$ có đồ thị $(C)$. Hai đường tiệm cận của đồ thị $\left( C \right)$ cùng với hai trục tọa độ tạo thành một hình thang vuông có diện tích $S$. Tính $S$.
Đáp án: 6

Lời giải: Ta thấy đồ thị hàm số có đúng một đường tiệm cận đứng là ${{d}_{1}}:x=2$.
Mặt khác $y=x+2+\dfrac{7}{x-2}$ nên đường thẳng ${{d}_{2}}:y=x+2$ là tiệm cận xiên của $(C)$.
Đường thẳng ${{d}_{2}}:y=x+2$ cắt trục $Oy$ tại $A(0;2)$.
Đường thẳng ${{d}_{1}}:x=2$ cắt ${{d}_{2}}:y=x+2$ tại $B\left( 2;4 \right)$.
Đường thẳng ${{d}_{1}}:x=2$ cắt trục $Ox$ tại $C(2;0)$.
Do đó hai đường tiệm cận của đồ thị $\left( C \right)$ cùng với hai trục tọa độ tạo thành một hình thang vuông $OABC$.

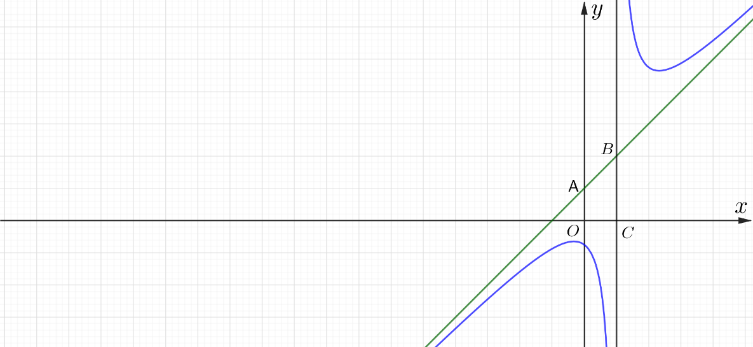
$\Rightarrow {{S}_{OABC}}=\dfrac{(OA+BC).OC}{2}=6$.