Cho hàm số f liên tục, f(x) >  – 1,  f(0) = 0 và thỏa mãn \( f'(x)\sqrt {{x^2} + 1} = 2x\sqrt {f(x) + 1} \) . Tính \(f( \sqrt 3 ) \)

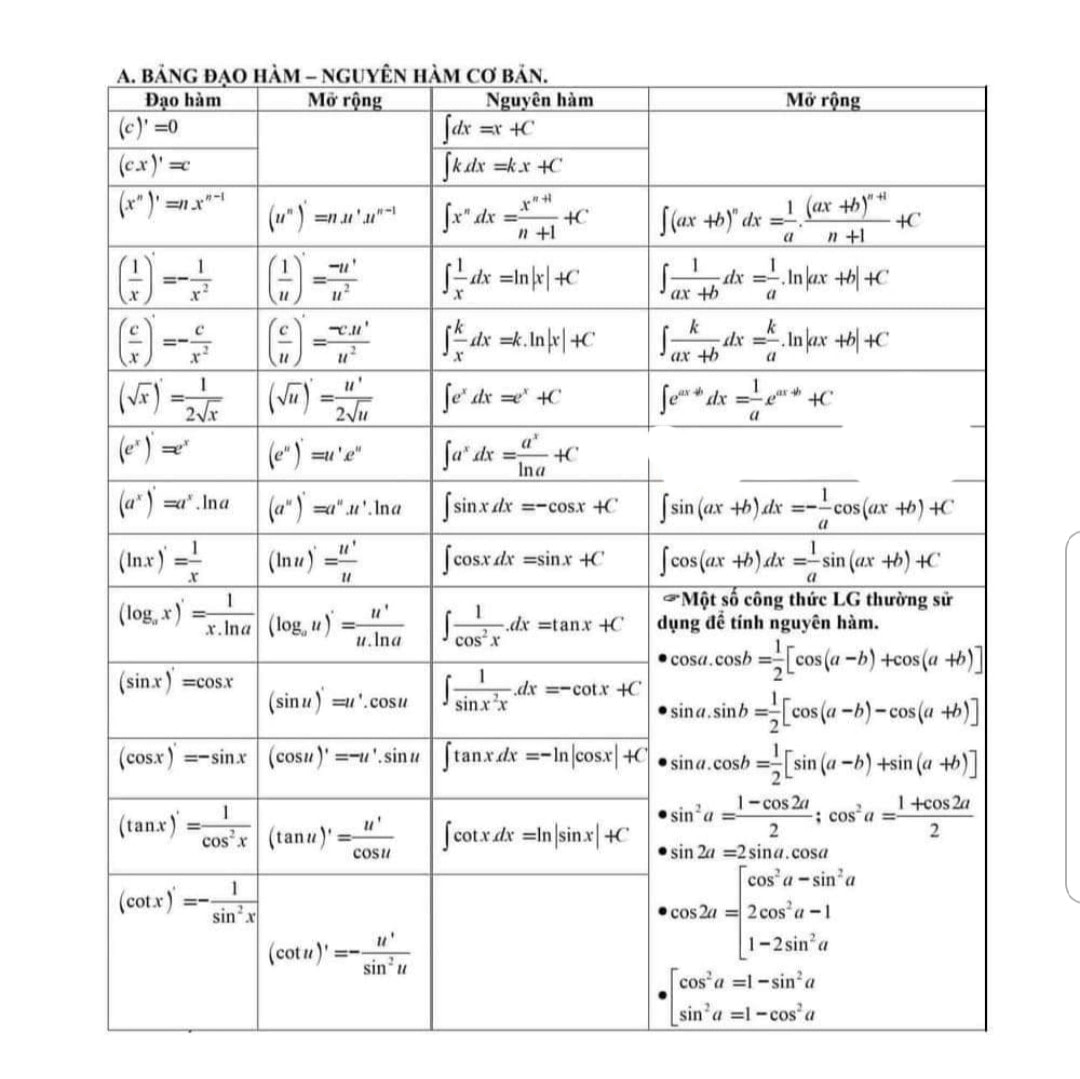
\( f'(x)\sqrt {{x^2} + 1} = 2x\sqrt {f(x) + 1} \Leftrightarrow \frac{{f'(x)}}{{\sqrt {f(x) + 1} }} = \frac{{2x}}{{\sqrt {{x^2} + 1} }} \Rightarrow \smallint \frac{{f'(x)}}{{\sqrt {f(x) + 1} }}dx = \smallint \frac{{2x}}{{\sqrt {{x^2} + 1} }}dx \Leftrightarrow \smallint \frac{{d\left( {f(x) + 1} \right)}}{{\sqrt {f(x) + 1} }} = \smallint \frac{{d({x^2} + 1)}}{{\sqrt {{x^2} + 1} }}\)

Mà \(\begin{array}{l}
f(0) = 0 \Rightarrow 2\sqrt {0 + 1} = 2\sqrt {{0^2} + 1} + C \Rightarrow C = 0\\
\Rightarrow \sqrt {f(x) + 1} = \sqrt {{x^2} + 1} \Leftrightarrow f(x) = {x^2} \Rightarrow f\left( {\sqrt 3 } \right) = {\left( {\sqrt 3 } \right)^2} = 3
\end{array}\)