Biết rằng hai điểm cực trị của đồ thị hàm số $y=\dfrac{{{x}^{2}}+2x-3}{{{x}^{2}}+1}$ cùng với điểm $I\left( -\sqrt{5};-\sqrt{5} \right)$ tạo thành một tam giác.

Bài toán gốc

Biết rằng hai điểm cực trị của đồ thị hàm số $y=\dfrac{{{x}^{2}}+2x-3}{{{x}^{2}}+1}$ cùng với điểm $I\left( -\sqrt{5};-\sqrt{5} \right)$ tạo thành một tam giác. Diện tích tam giác đó bằng (kết quả làm tròn đến hàng phần trăm)
Đáp án: 6,71

Lời giải: Tập xác định $\mathbb{R}$
+ ${y}’=\dfrac{\left( 2x+2 \right)\left( {{x}^{2}}+1 \right)-2x\left( {{x}^{2}}+2x-3 \right)}{{{\left( {{x}^{2}}+1 \right)}^{2}}}$ $=\dfrac{-2{{x}^{2}}+8x+2}{{{\left( {{x}^{2}}+1 \right)}^{2}}}$
${y}’=0\Leftrightarrow \left[ \begin{array}{l} x=2-\sqrt{5} \\ x=2+\sqrt{5} \end{array} \right.$.
Bảng biến thiên

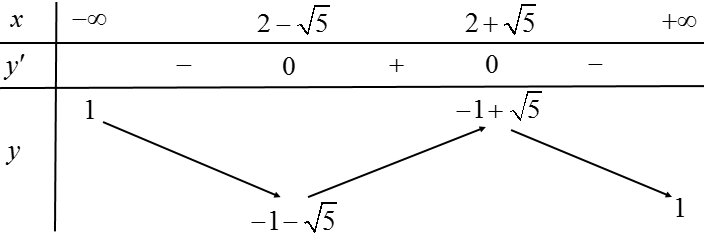
Vậy đồ thị hàm số có hai điểm cực trị là $A\left( 2-\sqrt{5};-1-\sqrt{5} \right)$ và $B\left( 2+\sqrt{5};-1+\sqrt{5} \right)$
Khi đó $\overrightarrow{AB}=\left( 2\sqrt{5};2\sqrt{5} \right)$ $\Rightarrow AB=2\sqrt{10}$; $\overrightarrow{AI}=\left( 2;-1 \right)$ $\Rightarrow AI=\sqrt{5}$; $\overrightarrow{IB}=\left( 2+2\sqrt{5};-1+2\sqrt{5} \right)$ $\Rightarrow IB=\sqrt{45+4\sqrt{5}}$.
Trong tam giác $\cos A=\dfrac{A{{B}^{2}}+A{{I}^{2}}-B{{I}^{2}}}{2AB.AI}$ $=\dfrac{40+5-45-4\sqrt{5}}{2.2\sqrt{10}.\sqrt{5}}=-\dfrac{1}{\sqrt{10}}$ $\Rightarrow \sin A=\dfrac{3}{\sqrt{10}}$.
Diện tích tam giác $ABI$ là: ${{S}_{ABI}}=\dfrac{1}{2}AB.AI.\sin A$ $=\dfrac{1}{2}.2\sqrt{10}.\sqrt{5}\dfrac{3}{\sqrt{10}}=3\sqrt{5}$ $\approx 6,71$.

Phân tích và Phương pháp giải

Đây là dạng bài toán ứng dụng đạo hàm để tìm tọa độ các điểm cực trị, sau đó sử dụng kiến thức hình học giải tích (hình học phẳng trong mặt phẳng tọa độ) để tính diện tích tam giác tạo bởi các điểm đó. Phương pháp giải bao gồm: (1) Tính đạo hàm y’ và giải phương trình y’=0 để tìm hoành độ cực trị. (2) Tính toán tung độ tương ứng để xác định tọa độ các điểm cực trị A và B. (3) Sử dụng công thức tính diện tích tam giác trong tọa độ (ví dụ: công thức $S = rac{1}{2} | ext{det}(\\\overrightarrow{AB}, \\\ riangle{AI})|$ hoặc công thức hình học cơ bản nếu tam giác có cạnh song song với trục tọa độ).

Bài toán tương tự

Tính diện tích tam giác tạo bởi hai điểm cực trị của đồ thị hàm số $y = \dfrac{x^2 – x + 1}{x^2 + 1}$ và điểm $I(1; 1)$.
Đáp án: 1/2
Lời giải ngắn gọn:
Tập xác định $\mathbb{R}$. Ta có $y’ = \dfrac{(2x – 1)(x^2 + 1) – 2x(x^2 – x + 1)}{({x^2 + 1})^2} = \dfrac{x^2 – 1}{({x^2 + 1})^2}$.
$y’ = 0 \Leftrightarrow x = 1$ hoặc $x = -1$.
Hai điểm cực trị là $A(1; y(1)) = A(1; 1/2)$ và $B(-1; y(-1)) = B(-1; 3/2)$.
Điểm $I(1; 1)$.
Ta nhận thấy điểm A và I có cùng hoành độ $x=1$, nên cạnh AI nằm trên đường thẳng $x=1$. Độ dài cạnh $AI = |y_I – y_A| = |1 – 1/2| = 1/2$.
Chiều cao $h$ của tam giác (khoảng cách từ B đến đường thẳng $x=1$) là $h = |x_B – 1| = |-1 – 1| = 2$.
Diện tích tam giác $S_{ABI} = \dfrac{1}{2} \cdot AI \cdot h = \dfrac{1}{2} \cdot \dfrac{1}{2} \cdot 2 = \dfrac{1}{2}$.