Một cái đập có mặt cắt có dạng hình thang cân cao 20 mét, đáy lớn rộng 50 mét và đáy nhỏ rộng 30 mét. Nước cách đỉnh đập 4 mét (tham khảo hình vẽ). Áp suất thuỷ tĩnh tác dụng lên đập được tính theo công thức ${F=9800 \int_0^{h_0} h(x) . k(x) {d} x({~N})}$, trong đó ${h(x)}$ và ${k(x)}$ lần lượt là chiều dài và độ sâu của lớp nước tại vị trí cách đáy ${x(m), h_0}$ là độ cao của nước trong hồ. Biết rằng ${F=a \cdot 10^7({~N})}$, tính ${a}$ (làm tròn kết quả đến hàng phần mười). 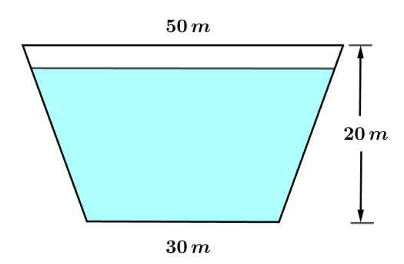
Lời giải
Trả lời: ${\mathbf{4 , 4}}$. Ta kẻ ${A B}$ song song với đáy và kí hiệu các điểm như hình. 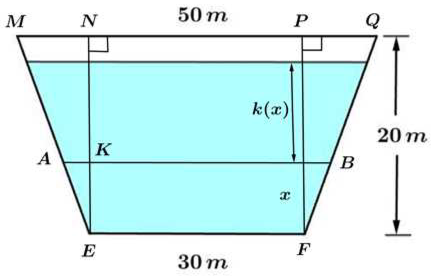 Vì nước cách đỉnh đập 4 m nên độ cao của nước trong hồ ${h_0=20-4=16({~m})}$. Khi đó, ${k(x)=16-x ; h(x)=A B}$. Vì mặt cắt của đập có dạng hình thang cân, nên khi kẻ ${\left\{\begin{array}{l}E N \perp M Q \\ F P \perp M Q\end{array}\right.}$ thì ${E N P F}$ là hình chữ nhật và ${\Delta E M N=\Delta F P Q}$. Suy ra ${M N=\frac{M Q-N P}{2}=\frac{50-30}{2}=10({~m})}$. Suy ra ${h(x)=A B=30+2 A K}$. Trong tam giác ${E M N}$, ta có ${A K / / M N}$ nên áp dụng định lý Thalès, ta có ${\frac{E K}{E N}=\frac{A K}{M N} \Rightarrow A K=\frac{E K \cdot M N}{E N}=\frac{10 x}{20}=\frac{1}{2} x}$. Suy ra ${h(x)=30+x}$. Khi đó áp suất tĩnh thủy tác dụng lên đập nước là ${F=9800 \int_0^{16}(16-x)(30+x) {d} x=44322133.33 \approx 4,4.10^7({~N})}$
Vì nước cách đỉnh đập 4 m nên độ cao của nước trong hồ ${h_0=20-4=16({~m})}$. Khi đó, ${k(x)=16-x ; h(x)=A B}$. Vì mặt cắt của đập có dạng hình thang cân, nên khi kẻ ${\left\{\begin{array}{l}E N \perp M Q \\ F P \perp M Q\end{array}\right.}$ thì ${E N P F}$ là hình chữ nhật và ${\Delta E M N=\Delta F P Q}$. Suy ra ${M N=\frac{M Q-N P}{2}=\frac{50-30}{2}=10({~m})}$. Suy ra ${h(x)=A B=30+2 A K}$. Trong tam giác ${E M N}$, ta có ${A K / / M N}$ nên áp dụng định lý Thalès, ta có ${\frac{E K}{E N}=\frac{A K}{M N} \Rightarrow A K=\frac{E K \cdot M N}{E N}=\frac{10 x}{20}=\frac{1}{2} x}$. Suy ra ${h(x)=30+x}$. Khi đó áp suất tĩnh thủy tác dụng lên đập nước là ${F=9800 \int_0^{16}(16-x)(30+x) {d} x=44322133.33 \approx 4,4.10^7({~N})}$
Vậy ${a=4,4}$.
Một cái đập có mặt cắt có dạng hình thang cân cao 20 mét, đáy lớn rộng 50 mét và đáy nhỏ rộng 30 mét
Ngày Thuộc chủ đề:Trắc nghiệm Ứng dụng Tích phân
