Cho các số liệu thống kê ghi trong bảng sau: Thời gian (phút) đi từ nhà đến trường của bạn A trong 35 ngày.
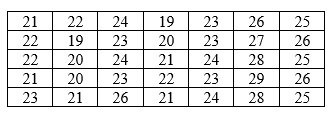
Ta lập được bảng mẫu số liệu ghép nhóm với các nhóm: $\left[ 19,21 \right);\left[ 21;23 \right);\left[ 23;25 \right);\left[ 25;27 \right);\left[ 27;29 \right)$.
Hãy tìm khoảng tứ phân vị của mẫu số liệu ghép nhóm đã lập (làm tròn kết quả đến hàng phần mười)
Lời giải
Trả lời: 3,8
Lập bảng mẫu số liệu ghép nhóm với các nhóm:
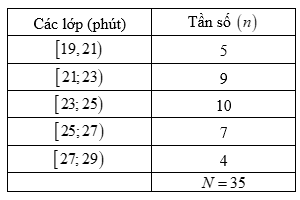
Cỡ mẫu $n=35$. Gọi ${{x}_{1}},{{x}_{2}},…,{{x}_{35}}$ là thời gian đi đến trường của ban A trong 35 ngày và giả sử dãy này đã được sắp xếp theo thứ tự tăng dần. Khi đó, trung vị là ${{x}_{18}}$.
Do giá trị ${{x}_{18}}$ thuộc nhóm $\left[ 23;25 \right)$ nên nhóm này chứa trung vị. Do đó, $p=3;{{a}_{3}}=23;{{m}_{3}}=10;{{m}_{1}}+{{m}_{2}}=14;{{a}_{4}}-{{a}_{3}}=2$ và ta có:
${{Q}_{2}}={{M}_{e}}=23+\dfrac{\dfrac{35}{2}-14}{10}.2=23,7$.
Tứ phân vị thứ nhất ${{Q}_{1}}={{x}_{9}}$. Do giá trị ${{x}_{9}}$ thuộc nhóm $\left[ 21;23 \right)$ nên nhóm này chứa ${{Q}_{1}}$. Do đó, $p=2;{{a}_{2}}=21;{{m}_{2}}=9;{{m}_{1}}=5;{{a}_{3}}-{{a}_{2}}=2$ và ta có:
${{Q}_{1}}=21+\dfrac{\dfrac{35}{4}-5}{9}.2\approx 21,8$.
Tứ phân vị thứ ba ${{Q}_{3}}={{x}_{27}}$. Do hai giá trị ${{x}_{27}}$ thuộc nhóm $\left[ 25;27 \right)$ nên nhóm này chứa ${{Q}_{3}}$. Do đó, $p=4;{{a}_{4}}=25;{{m}_{4}}=7;{{m}_{1}}+{{m}_{2}}+{{m}_{3}}=24;{{a}_{5}}-{{a}_{4}}=2$ và ta có:
${{Q}_{3}}=25+\dfrac{\dfrac{3.35}{4}-24}{7}.2\approx 25,6$.
Vậy $\Delta Q=25,6-21,8=3,8$
