Cho bảng số liệu thống kê thời gian (phút) hoàn thành một bài tập toán của một học sinh lớp 11.
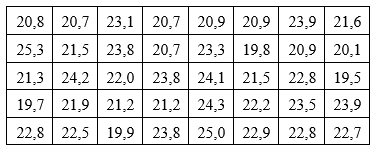
Ta lập được bảng mẫu số liệu ghép nhóm với các nhóm
$\left[ 19,5;20,5 \right);\left[ 20,5;21,5 \right);\left[ 21,5;22,5 \right);\left[ 22,5;23,5 \right);\left[ 23,5;24,5 \right),\left[ 24,5;25,5 \right]$.
Hãy tìm khoảng tứ phân vị của mẫu số liệu ghép nhóm đã lập.
Lời giải
Trả lời: 2,7
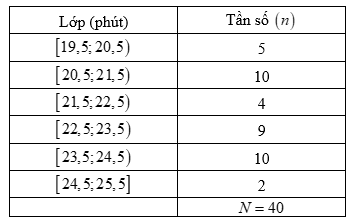
Cỡ mẫu $n=40$. Gọi ${{x}_{1}},{{x}_{2}},…,{{x}_{40}}$ là thời gian hoàn thành bài tập Toán của 40 học sinh và giả sử dãy này đã được sắp xếp theo thứ tự tăng dần. Khi đó, trung vị là $\dfrac{{{x}_{20}}+{{x}_{21}}}{2}$.
Do hai giá trị ${{x}_{20}},{{x}_{21}}$ thuộc nhóm $\left[ 22,5;23,5 \right)$ nên nhóm này chứa trung vị. Do đó, $p=4;{{a}_{4}}=22,5;{{m}_{4}}=9;{{m}_{1}}+{{m}_{2}}+{{m}_{3}}=19;{{a}_{5}}-{{a}_{4}}=1$ và ta có: ${{Q}_{2}}={{M}_{e}}=22,5+\dfrac{\dfrac{40}{2}-19}{9}.1\approx 22,6$.
Tứ phân vị thứ nhất ${{Q}_{1}}=\dfrac{{{x}_{10}}+{{x}_{11}}}{2}$. Do hai giá trị ${{x}_{10}},{{x}_{11}}$ thuộc nhóm $\left[ 20,5;21,5 \right)$ nên nhóm này chứa ${{Q}_{1}}$. Do đó, $p=2;{{a}_{2}}=20,5;{{m}_{2}}=10;{{m}_{1}}=5;{{a}_{3}}-{{a}_{2}}=1$ và ta có: ${{Q}_{1}}=20,5+\dfrac{\dfrac{40}{4}-5}{10}.1=21$.
Tứ phân vị thứ ba ${{Q}_{3}}=\dfrac{{{x}_{30}}+{{x}_{31}}}{2}$. Do hai giá trị ${{x}_{30}},{{x}_{31}}$ thuộc nhóm $\left[ 23,5;24,5 \right)$ nên nhóm này chứa ${{Q}_{3}}$. Do đó, $p=5;{{a}_{5}}=23,5;{{m}_{5}}=10;{{m}_{1}}+{{m}_{2}}+{{m}_{3}}+{{m}_{4}}=28;{{a}_{6}}-{{a}_{5}}=1$ và ta có: ${{Q}_{3}}=23,5+\dfrac{\dfrac{3.40}{4}-28}{10}.1=23,7$.
Ta có $\Delta Q={{Q}_{3}}-{{Q}_{1}}=2,7$
