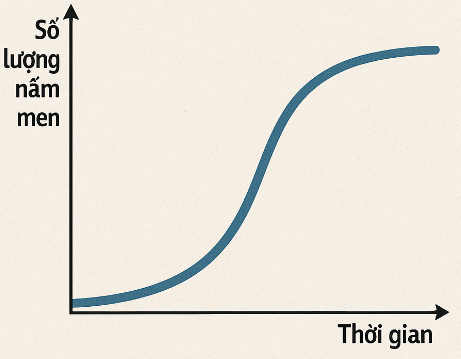
Giả sử số lượng của một quần thể nấm men tại môi trường nuôi cấy trong phòng thí nghiệm được mô hình hoá bằng hàm số $P\left( t \right)=\frac{a}{b+{{\text{e}}^{-0,75t}}}$, trong đó thời gian $t$ được tính bằng giờ. Tại thời điểm ban đầu $t=0$, quần thể có 20 tế bào và tăng với tốc độ 12 tế bào/giờ. Theo mô hình này số lượng nấm men không vượt quá bao nhiêu con?
Lời giải
Đáp án: 100
Ta có: ${P}’\left( t \right)=\frac{0,75a{{\text{e}}^{-0,75t}}}{{{\left( b+{{\text{e}}^{-0,75t}} \right)}^{2}}}\,,\,\,t\ge 0$.
Theo đề bài, ta có: $P\left( 0 \right)=20$ và ${P}’\left( 0 \right)=12$.
Do đó, ta có hệ phương trình: $\left\{ \begin{array}{*{35}{l}}
\frac{a}{b+1}=20 \\
\frac{0,75a}{{{\left( b+1 \right)}^{2}}}=12 \\
\end{array}\Leftrightarrow \left\{ \begin{array}{*{35}{l}}
a=20\left( b+1 \right) \\
\frac{15}{b+1}=12 \\
\end{array} \right. \right.$.
Giải hệ phương trình này, ta được $a=25$ và $b=\frac{1}{4}$.
Khi đó, ${P}’\left( t \right)=\frac{18,75{{\text{e}}^{-0,75t}}}{{{\left( \frac{1}{4}+{{\text{e}}^{-0,75t}} \right)}^{2}}}>0\,,\,\,\forall t\ge 0$, tức là số lượng nấm men luôn tăng.
Tuy nhiên, do $\underset{t\to +\infty }{\mathop{\lim }}\,P\left( t \right)=\underset{t\to +\infty }{\mathop{\lim }}\,\frac{25}{\frac{1}{4}+{{\text{e}}^{-0.75t}}}=100$ nên số lượng nấm men tăng nhưng không vượt quá 100 tế bào.
