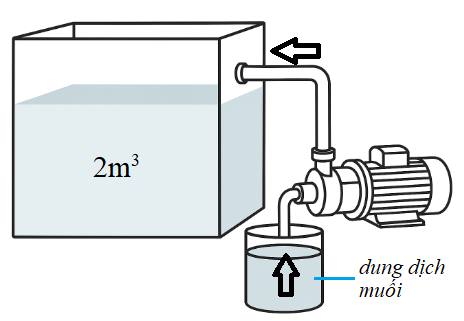
Một bể chứa $2{{m}^{3}}$ nước tinh khiết. Người ta bơm vào bể đó nước muối có nồng độ không đổi với tốc độ $20$lít/phút. Nồng độ muối trong bể sau $t$ phút (tính bằng tỉ số của khối lượng muối có trong bể và thể tích nước trong bể, đơn vị gam/lít) là một hàm số $f\left( t \right)$, thời gian tính bằng phút. Biết rằng tiệm cận ngang của đồ thị hàm số $f\left( t \right)$ là $y=10$. Nồng độ muối trong bể sau khi bơm được 1 giờ là bao nhiêu?
Lời giải
Đáp án: 3,75.
Giả sử nước muối bơm vào có nồng độ $a$ gam/lít.
Sau $t$ phút ta có khối lượng muối trong bể là $20at$ (gam).
Thể tích của lượng nước trong bể sau $t$ phút là $2000+20t$ (lít).
Vậy nồng độ muối sau $t$ phút là $f\left( t \right)=\frac{20at}{2000+20t}=\frac{at}{100+t}$ (gam/lít).
Ta có $\underset{t\to +\infty }{\mathop{\lim }}\,f\left( t \right)=\underset{t\to +\infty }{\mathop{\lim }}\,\frac{at}{100+t}=a$, nên đồ thị hàm số $f\left( t \right)$ có tiệm cận ngang là $y=a$. Suy ra $a=10$.
Do đó hàm nồng độ muối trong bể sau khi bơm được $t$ phút là $f\left( t \right)=\frac{10t}{100+t}$.
Nồng độ muối sau $1$ giờ bơm là $f\left( 60 \right)=\frac{10.60}{100+60}=3,75$ (gam/lít).
