Khi một vật lạ mắc kẹt trong khí quản khiến ta phải ho, cơ hoành đẩy lên trên gây ra tăng áp lực trong phổi, theo đó cuống họng co thắt làm hẹp khí quản khiến không khí đi qua mạnh hơn. Đối với một lượng không khí bị đẩy ra trong một khoảng thời gian cố định, khí quản càng nhỏ thì luồng không khí càng đẩy ra nhanh hơn. Vận tốc luồng khí thoát ra càng cao, lực tác động lên vật lạ càng lớn.
Qua nghiên cứu một số trường hợp, người ta nhận thấy vận tốc ${v}$ của luồng khí liên hệ với bán kính ${x}$ của khí quản theo công thức: $v(x)=k\left( {{x}_{0}}-x \right)\cdot {{x}^{2}}\text{ voi }\dfrac{1}{2}{{x}_{0}}\le x\le {{x}_{0}}$
trong đó ${k}$ là hằng số ${(k{>}0)}$ và ${x_0}$ là bán kính khí quản ở trạng thái bình thường
(Theo James Stewart, J. (2015). Calculus. Cengage Learning).
Khi đó ${x=}$ $…………$ ${x_0}$ thì vận tốc luồng khí của một cơn ho trong trường hợp này
là lớn nhất (làm tròn kết quả đến hàng phần trăm).
Lời giải
Trả lời: 0,67
Xét hàm số ${f(x)=\left(x_0-x\right) x^2}$ với ${x_0}$ cố định và ${\dfrac{1}{2} x_0 \leq x \leq x_0}$.
Do ${k}$ là hằng số dương nên vận tốc của luồng khí của một cơn ho lớn nhất khi ${f(x)}$ đạt giá trị lớn nhất.
Ta có:
$f(x)=-{{x}^{3}}+{{x}_{0}}{{x}^{2}};{{f}^{\prime }}(x)=-3{{x}^{2}}+2{{x}_{0}}x;{{f}^{\prime }}(x)=0\Leftrightarrow x=0\text{ hoac }x=\dfrac{2}{3}{{x}_{0}}.$
Bảng biến thiên:
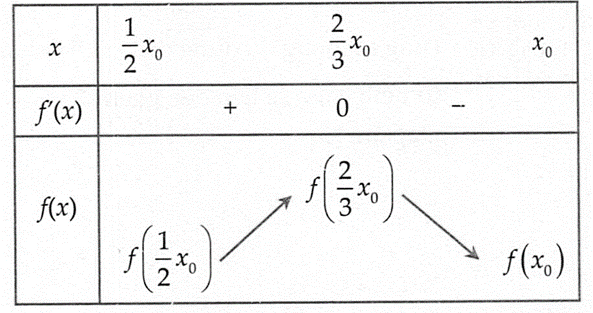
Dựa vào bảng biến thiên, ta có: ${\max _{\left[\dfrac{1}{2} x_0 ; x_0\right]} f(x)=f\left(\dfrac{2}{3} x_0\right)}$.
Vậy vận tốc của luồng khí của một con ho lớn nhất khi ${x=\dfrac{2}{3} x_0}$.
Đáp án: $\dfrac{2}{3}\approx 0,67$.
