Một cái hồ rộng có hình chữ nhật

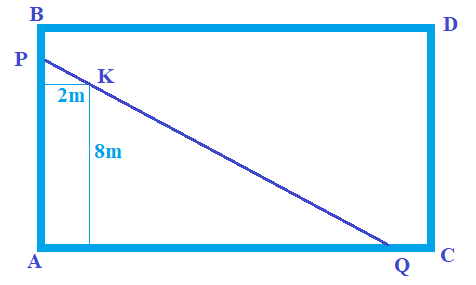
Một cái hồ rộng có hình chữ nhật. Tại một góc hồ người ta đóng một cái cọc ở vị trí ${K}$ cách bờ ${A B}$ là ${2 m}$ và cách bờ ${A C}$ là ${8 m}$, rồi dùng một cây sào thẳng ${P Q}$ ngăn một góc của hồ để thả bèo (như hình vẽ). Tính chiều dài ngắn nhất của cây sào để cây sào có thể chạm vào hai bờ ${A B, A C}$ và cây cọc (kết quả làm tròn đến hàng đơn vị của mét).

Lời giải

Đáp án: 174.

Đặt ${A P=a, A Q=b(a{>}8 ; b{>}2)(m)}$.

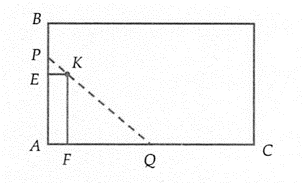
Gọi ${E}$ và ${F}$ lần lượt là hình chiếu vuông góc của ${K}$ xuống ${A B}$ và ${A C}$. Suy ra ${K E=2 m, K F=8 {m}}$.

Ta có: ${\dfrac{K E}{A Q}=\dfrac{P K}{P Q} ; \dfrac{K F}{A P}=\dfrac{Q K}{P Q}}$ ${\Rightarrow \dfrac{K F}{A P}+\dfrac{K E}{A Q}=1}$ hay ${\dfrac{8}{a}+\dfrac{2}{b}=1}$.

Vi ${\dfrac{8}{a}+\dfrac{2}{b}=1}$ nên ${b=\dfrac{2 a}{a-8}}$.

Khi đó ${P Q^2=a^2+b^2=a^2+\left(\dfrac{2 a}{a-8}\right)^2}$.

Xét hàm số ${y=f(a)=a^2+\left(\dfrac{2 a}{a-8}\right)^2}$ trên khoảng ${(8 ;+\infty)}$.

Ta có:

${{f}^{\prime }}(a)=2a+\dfrac{4a}{a-8}\cdot \dfrac{-16}{{{(a-8)}^{2}}}=\dfrac{2a\left[ {{(a-8)}^{3}}-32 \right]}{{{(a-8)}^{3}}};{{f}^{\prime }}(a)=0\Rightarrow {{(a-8)}^{3}}=32\Rightarrow a=8+\sqrt[3]{32}{>}8.$ Bảng biến thiên:

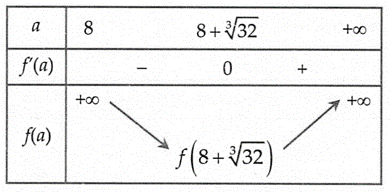
Do đó ${\min _{(8,+\infty)} f(a)=f(8+\sqrt[3]{32}) \approx 174,43}$.

Vậy chiều dài ngắn nhất của cây sào có thể chạm vào hai bờ ${A B, A C}$ và cây cọc là 174 m.