Cho một tấm bìa hình vuông có cạnh $2m$. Từ tấm bìa này làm một mô hình kim tự tháp Ai Cập, người ta cắt bỏ bốn tam giác cân bằng nhau có cạnh đáy là các cạnh của hình vuông rồi gấp lên và ghép lại thành một hình chóp tứ giác đều. Thể tích của mô hình lớn nhất khi cạnh đáy của mô hình bằng $\dfrac{a\sqrt{2}}{b}\left( m \right)$ ( $a,b\in \mathbb{Z};a,b$ nguyên tố cùng nhau). Tính tổng ${{a}^{2}}+{{b}^{2}}$ ?
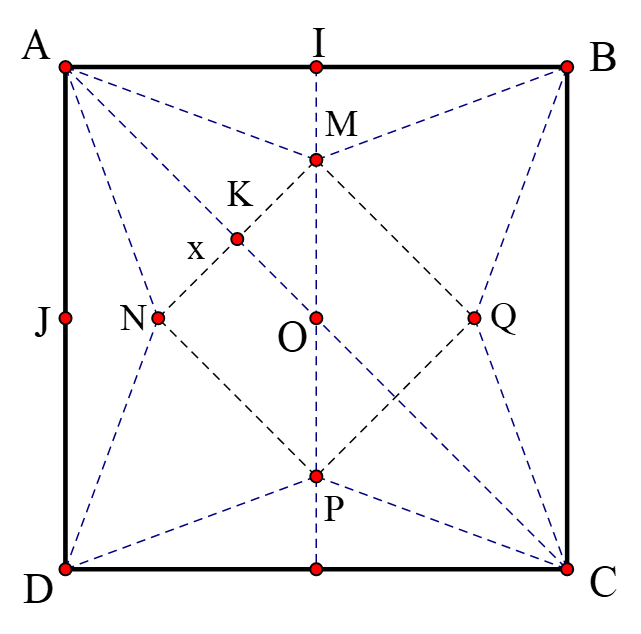
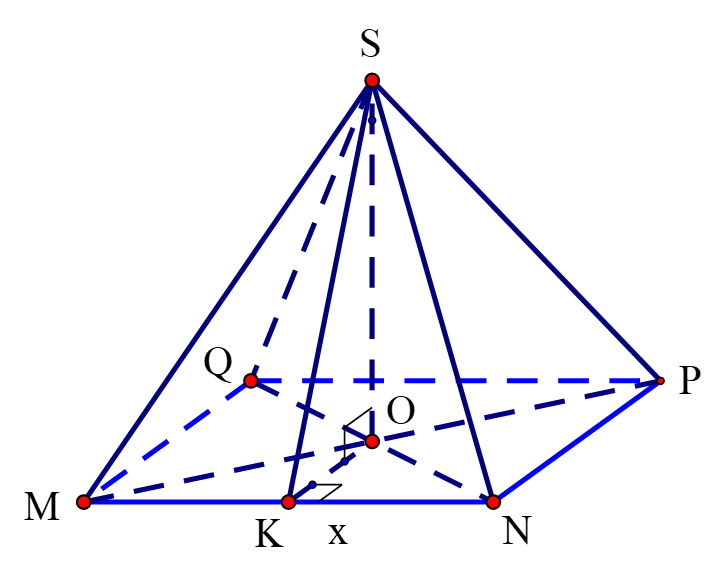 Ta thấy thể tích của mô hình lớn nhất khi cạnh đáy của mô hình là $x=\dfrac{4\sqrt{2}}{5}\Rightarrow a=4,b=5\Rightarrow {{a}^{2}}+{{b}^{2}}=41$.
Ta thấy thể tích của mô hình lớn nhất khi cạnh đáy của mô hình là $x=\dfrac{4\sqrt{2}}{5}\Rightarrow a=4,b=5\Rightarrow {{a}^{2}}+{{b}^{2}}=41$.
