Sau khi phát hiện một bệnh dịch, các chuyên gia y tế ước tính số người nhiễm bệnh kể từ ngày xuất hiện bệnh nhân đầu tiên đến ngày thứ ${t}$ là ${N(t)=45 t^2-t^3, 0 \leq t \leq 30}$ (người). Nếu xem ${N^{\prime}(t)}$ là tốc độ truyền bệnh (người/ ngày) tại thời điểm ${t}$ thì tốc độ truyền bệnh lớn nhất sẽ vào ngày thứ bao nhiêu?
Lời giải
Đáp án: 15.
Ta có: ${N(t)=45 t^2-t^3, 0 \leq t \leq 30}$;
${{N}^{\prime }}(t)=90t-3{{t}^{2}},{{N}^{\prime \prime }}(t)=90-6t{{N}^{\prime \prime }}(t)=0\Leftrightarrow 90-6t=0\Leftrightarrow t=15$
Bảng biến thiên:
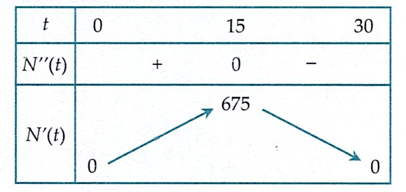
Vậy tốc độ truyền bệnh lớn nhất sẽ vào ngày thứ 15.
