Khi chất thải hữu cơ được đổ vào một cái ao, quá trình ôxy hóa xảy ra sẽ làm giảm hàm lượng ôxy trong nước

Khi chất thải hữu cơ được đổ vào một cái ao, quá trình ôxy hóa xảy ra sẽ làm giảm hàm lượng ôxy trong nước. Tuy nhiên, theo thời gian, tự nhiên sẽ phục hồi lại mức ôxy về giá trị bình thường. Trong đồ thị kèm theo, ${P(t)}$ cho biết phần trăm hàm lượng ôxy (so với mức bình thường) sau ${t}$ ngày kể từ khi chất thải được đổ vào ao.

Giả sử hàm số cho hàm lượng ôxy là $P(t)=100\dfrac{{{t}^{2}}+10t+100}{{{t}^{2}}+20t+100}$ ( $%$ mức bình thường), $\text{t}\ge \text{0}\text{. }$

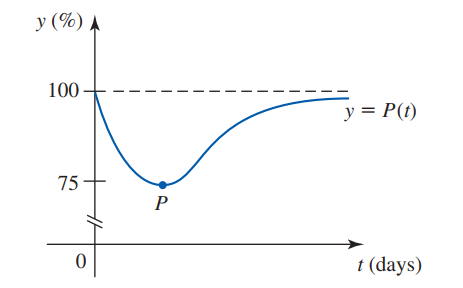
Khi đó tọa độ của điểm $P\left( a;b \right)$ trên đồ thị là điểm cực trị của đồ thị hàm số ${P(t)}$. Tính $a+b$ ?

Lời giải

Trả lời: 85

Ta có: $P\prime (t)=\dfrac{(2t+10)\left( {{t}^{2}}+20t+100 \right)-(2t+20)\left( {{t}^{2}}+10t+100 \right)}{{{\left( {{t}^{2}}+20t+100 \right)}^{2}}}$

Khi đó ${{P}^{\prime }}(t)=0\Leftrightarrow (2t+10)\left( {{t}^{2}}+20t+100 \right)-(2t+20)\left( {{t}^{2}}+10t+100 \right)=0$

$\Rightarrow 10{{t}^{2}}-1000=0\Rightarrow {{t}^{2}}=100\Rightarrow t=10\quad (t\ge 0)$

Lập bảng biến thiên ta có $t=10$ là điểm cực tiểu của hàm số

Thay ${t=10}$ vào ${P(t)}$ : $P(10)=100\dfrac{{{10}^{2}}+10\cdot 10+100}{{{10}^{2}}+20\cdot 10+100}=100\dfrac{100+100+100}{100+200+100}=100\dfrac{300}{400}=75.$

Vậy điểm ${P}$ có tọa độ $(10;75)$