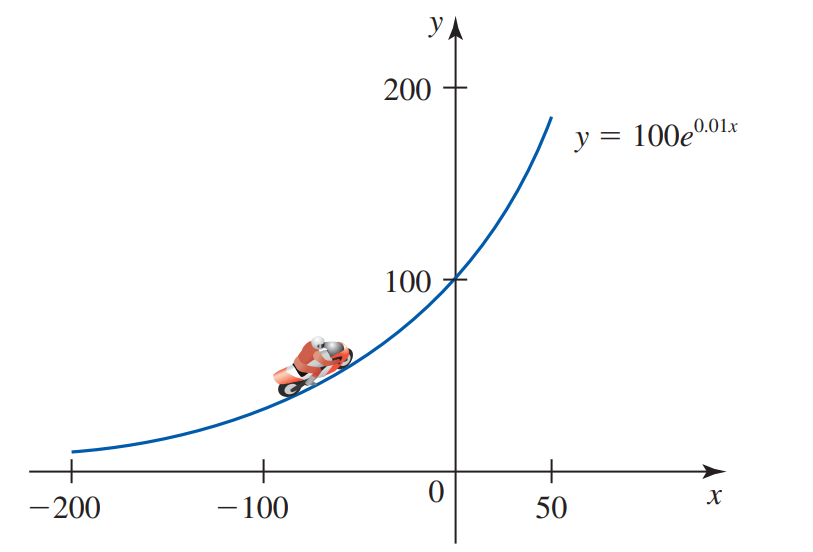
Một tay lái mô tô nặng 180 (lb), di chuyển với vận tốc không đổi 30 dặm/giờ, thực hiện một khúc cua trên đường cho bởi đồ thị $y=100{{e}^{0,01x}},\quad -200\le x\le 50$
Có thể chứng minh rằng độ lớn của lực pháp tuyến tác dụng lên tay lái mô tô xấp xỉ
$F(x)=\dfrac{10890{{e}^{0,1x}}}{{{\left( 1+100{{e}^{0,2x}} \right)}^{3/2}}}$ (đơn vị lb)
Hãy tìm lực pháp tuyến lớn nhất tác dụng lên tay lái trong suốt khúc cua (làm tròn kết quả đến hàng đơn vị)
Lời giải
Trả lời: 419
Đặt $u={{e}^{0,2x}}\left( \Rightarrow {{e}^{0,1x}}={{u}^{1/2}} \right)$ khi đó $F(x)=10890\dfrac{{{u}^{1/2}}}{{{(1+100u)}^{3/2}}}$
Để tìm cực đại, xét $G(u)=\dfrac{{{u}^{1/2}}}{{{(1+100u)}^{3/2}}},\quad u{>}0$
Tính $\ln G=\dfrac{1}{2}\ln u-\dfrac{3}{2}\ln (1+100u)\Rightarrow \left( \ln G \right)\prime =\dfrac{1}{2u}-\dfrac{150}{1+100u}$
Cho đạo hàm bằng 0: $\dfrac{1}{2u}=\dfrac{150}{1+100u}\Rightarrow 1+100u=300u\Rightarrow 200u=1\Rightarrow u=0,005$
Lập bảng biến thiên cho hàm số $G(u),u{>}0$ ta có được hàm số đạt cực đại tại $u=0,005$
Trả về biến ${x}$ : ${{e}^{0,2x}}=0,005\Rightarrow 0,2x=\ln (0,005)\approx -5,298\Rightarrow x\approx -26,49.$
(thuộc miền ${[-200,50]}$ ).
Giá trị cực đại ${{F}_{C}}=10890\dfrac{\sqrt{0,005}}{{{(1+100\cdot 0,005)}^{3/2}}}=10890\dfrac{0,07071}{1,{{5}^{3/2}}}=10890\dfrac{0,07071}{1,8371}\approx 419,4lb$
– Lực pháp tuyến đạt cực đại khi ${x \approx-26.5}$.
– Giá trị cực đại là khoảng $419$ (lb). ${}$
